设
是椭圆
的两点，
，
，且
，椭圆离心率
，短轴长为2，O为坐标原点．
（1）求椭圆方程；
（2）若存在斜率为
的直线AB过椭圆的焦点
（
为半焦距），求的值；
（3）试问
的面积是否为定值？若是，求出该定值；若不是，说明理由．
若函数y= f(2x＋1)的定义域为[ 1，2 ]，求f (x)的定义域
某良种培育基地正在培育一种小麦新品种A，将其与原有的一个优良品种B进行对照
试验，两种小麦各种植了25亩，所得亩产数据（单位：千克）如下：
品种A:357，359，367，368，375，388，392，399，400，405，414，
415，421，423，423，427，430，430，434，443，445，451，454
品种B：363，371，374，383，385，386，391，392，394，395，397
397，400，401，401，403，406，407，410，412，415，416，422，430
（Ⅰ）完成所附的茎叶图
（Ⅱ）用茎叶图处理现有的数据，有什么优点？
（Ⅲ）通过观察茎叶图，对品种A与B的亩产量及其稳定性进行比较，写出统计结论。
定义在D上的函数y=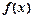
,集合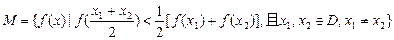
.
判断函数g(x)=2x与h(x)=lgx是否属于M,并证明你的结论.
己知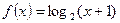
，当点
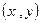在函数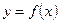
的图象上时，点
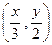在函数
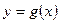的图象上。
（1）写出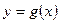的解析式；
（2）求
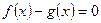方程的根
已知函数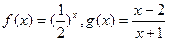
，试判断H(x)=f(-2x)+g(x)在
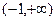的单调性并加以证明