如图1，已知∠DAC=90°，△ABC是等边三角形，点P为射线AD上任意一点（点P与点A不重合），连结CP，将线段CP绕点C顺时针旋转60°得到线段CQ，连结QB并延长交直线AD于点E．
（1）如图1，猜想∠QEP= °；
（2）如图2，3，若当∠DAC是锐角或钝角时，其它条件不变，猜想∠QEP的度数，选取一种情况加以证明；
（3）如图3，若∠DAC=135°，∠ACP=15°，且AC=4，求BQ的长．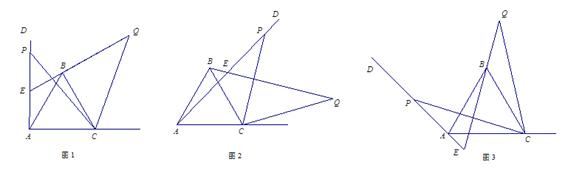
已知:在△ABC中，∠B <∠C, AD平分∠BAC，AE⊥BC，垂足为点E。 ∠B=380,∠C=700。
求∠DAE的度数
试写出∠DAE与∠B、∠C之间的一般等量关系式（只写结论）
通常把一个多边形每一个顶点处的一个外角的和叫做多边形的外角和。试证明三角形的外角和等于3600
已知：如图∠1、∠2、∠3是△ABC的三个外角
求证：
证明：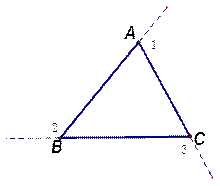
已知：△ABC中 AB=5，BC=2a+1，AC="12" 求a的取值范围
如果a="6" 那么请判断：△ABC是什么三角形？（友情提示：可以按角分类或按边分类）
在平面直角坐标系中的位置如图所示．将向右平移5个单位后再向下平移3个单位得到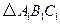
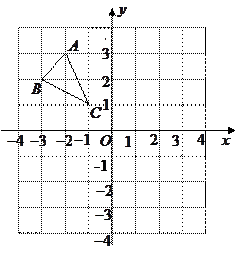
作出
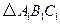
写出
上任意一点P(x,y)经平移后对应点为P1的坐标求
的面积
已知：DC∥AB DF平分∠CDB ，BE平分∠
ABD
求证 BE∥DF在空格处填角 括号内填推理的依据
证明∵DC∥AB（已知）
∴∠ABD=
（）
又∵DF平分∠CDB BE平分∠ABD（已知）
∴∠1=
∠2=（）
∴∠1=∠2（）
∴BE∥DF（）