如图是某市3月1日至14日的空气质量指数趋势图.空气质量指数小于100表示空气质量优良,空气质量指数大于200表示空气重度污染.某人随机选择3月1日至3月13日中的某一天到达该市,并停留2天.
(1)求此人到达当日空气质量优良的概率;
(2)求此人在该市停留期间只有1天空气重度污染的概率;
(3)由图判断从哪天开始连续三天的空气质量指数方差最大?(结论不要求证明)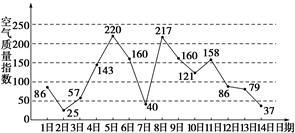
(本小题满分15分)设函数 ,直线
,直线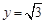 与函数
与函数 图象相邻两交点的距离为
图象相邻两交点的距离为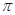 .
.
(Ⅰ)求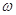 的值;
的值;
(Ⅱ)在 中,角
中,角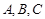 所对的边分别是
所对的边分别是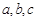 ,若点
,若点 是函数
是函数 图像的一个对称中
图像的一个对称中
心,且 ,求
,求 面积的最大值.
面积的最大值.
(本题满分14分 )已知函数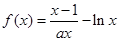 (
( )
)
(Ⅰ)求函数 的单调区间;
的单调区间;
(Ⅱ)当 时,求
时,求 在
在 上的最大值和最小值(
上的最大值和最小值(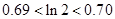 );
);
(Ⅲ)求证: .
.
如图,已知椭圆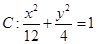 ,点
,点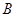 是其下顶点,过点
是其下顶点,过点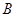 的直线交椭圆
的直线交椭圆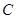 于另一 点
于另一 点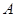 (
(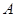 点在
点在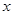 轴下方),且线段
轴下方),且线段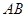 的中点
的中点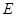 在直线
在直线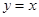 上.
上.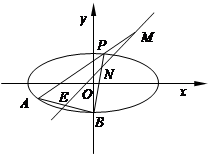
(Ⅰ)求直线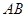 的方程;
的方程;
(Ⅱ)若点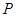 为椭圆
为椭圆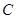 上异于
上异于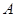 、
、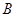 的动点,且直线
的动点,且直线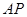 ,
,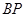 分别交直线
分别交直线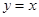 于点
于点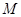 、
、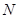 ,证明:
,证明: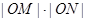 为定值.
为定值.
(本小题满分15分)如图,三棱柱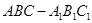 中,
中,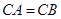 ,
,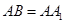 ,
,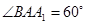 .
.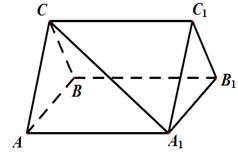
(Ⅰ) 证明: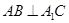 ;
;
(Ⅱ)若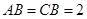 ,
,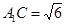 ,求二面角
,求二面角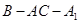 的余弦值.
的余弦值.
已知数列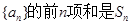 ,且
,且 .
.
(Ⅰ)求数列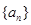 的通项公式;
的通项公式;
(Ⅱ)设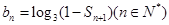 ,求适合方程
,求适合方程 的正整数
的正整数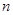 的值.
的值.