如图，已知△ABC三个顶点的坐标分别为A（-2，-1），B（-3，-3），C（-1，-3）,
（1）、画出△ABC向右平移三个单位的对应图形△
,并写出
的坐标；
（2）、画出△ABC关于原点O对称的△
，并写出
的坐标；
已知：如图1，一次函数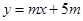
的图像与x轴、y轴分别交于点A、B，与函数
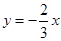的图像交于点C，点C的横坐标为－3．
（1）求点B的坐标；
（2）若点Q为直线OC上一点，且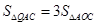
，求点Q的坐标；
（3）如图2，点D为线段OA上一点，∠ACD＝∠AOC．点P为x轴负半轴上一点，且点P到直线CD和直线CO的距离相等．
① 在图2中，只利用圆规作图找到点P的位置；
（保留作图痕迹，不得在图2中作无关元素．）
② 求点P的坐标．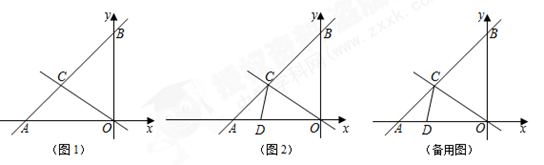
如图，在平面直角坐标系xOy中，一次函数y=kx+b的图象与x轴相交于点A（－３，０），与y轴交于点B，且与正比例函数y=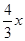
的图象交点为C（m，4）求：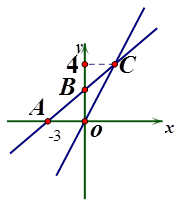
（1）一次函数y=kx+b的解析式；
（2）若点D在第二象限，△DAB是以AB为直角边的等腰直角三角形，直接写出点D的坐标。
（3）在x轴上求一点P使△POC为等腰三角形，请直接写出所有符合条件的点P的坐标．
如图，直线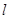
：
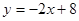分别与
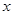轴、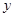
轴交于A、B两点，点C线段AB上，作CD⊥x轴于D, CD="2OD," 点E线段OB上,且AE=BE；
（1）填空：点C的坐标为（ ， ）；点E的坐标为（ ， ）；
（2）直线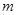
过点E，且将△AOB分成面积比为1：2的两部分，求直线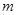的表达式；
（3）点P在x轴上运动，
①当PC+PE取最小值时，求点P的坐标及PC+PE的最小值；
②当PC-PE取最大值时，求点P的坐标及PC-PE的最大值；
如图，直线AB与x轴负半轴、y轴正半轴分别交于A、B两点，OA、OB的长度分别为a和b，且满足
，直线OQ与直线AB交于点Q，过A、B两点分别作AM⊥OQ于M，BN⊥OQ于N，若AM=9，BN=4，求MN的长．
如图，直线y =" 2x" + 3与x轴相交于点A，与y轴相交于点B．
（1）求A，B两点的坐标；
（2）过B点作直线BP与x轴的正半轴相交于P，且使OP = 2OA，求ΔABP的面积．