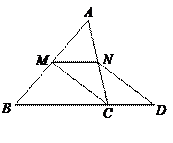平面直角坐标系中，抛物线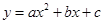
交
轴于A、B两点（点A在点B左侧），与
轴交于点C，点A、C的坐标分别为（-3,0），（0,3），对称轴直线
交轴于点E,点D为顶点.
（1）求抛物线的解析式；
（2）点P是直线AC下方的抛物线上一点，且
,，求点P的坐标；
（3）点M是第一象限内抛物线上一点，且∠MAC=∠ADE，求点M的坐标.
解分式方程：
．
解不等式：
≤
，并把它的解集在数轴上表示出来．
（本题满分
14分，其中第（1）小题3分，第（2）小题5分，第（3）小题6分）
如图，已知在△ABC中，AB=4，BC=2，以点B为圆心，线段BC长为半径的弧交边AC于点D，且∠DBC=∠BAC，P是边BC延长线上一点，过点P作PQ⊥BP，交线段BD的延长线于点Q．设CP=x，DQ=y．
（1）求CD的长；
（2）求y关于x的函数解析式，并写出它的定义域；
（3）当∠DAQ=2∠BAC时，求CP的值．
（本题满分12
分，其中第（1）小题3分，第（2）小题4分，第（3）小题5分）
如图，已知在直角坐标平面内，点A的坐标为（3,0），第一象限内的点P在直线y=2x上，∠PAO=45度．
（1）求点P的坐标；
（2）如果二次函数的图像经过P、O、A三点，求这个二次函数的解析式，并写出它的图像的顶点坐标M；
（3）如果将第（2）小题中的二次函数的图像向上或
向下平移，使它的顶点落在直线y=2x上的点Q处，求△APM与△APQ的面积之比．
（本题满分12分，其中每小题各6分）
已知：如图，在△ABC中，M是边AB的中点，D是边BC延长线上一点，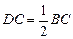
，DN∥CM，交边AC于点N．
（1）求证：MN∥BC；
（2）当∠ACB为何值时，四边形BDN
M是等腰梯形？并证明你的猜想．