已知椭圆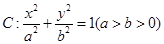 的焦点为
的焦点为 ,点
,点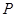 是椭圆
是椭圆 上的一点,
上的一点,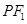 与
与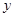 轴的交点
轴的交点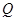 恰为
恰为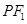 的中点,
的中点,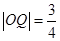 .
.
(1)求椭圆 的方程;
的方程;
(2)若点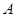 为椭圆的右顶点,过焦点
为椭圆的右顶点,过焦点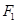 的直线与椭圆
的直线与椭圆 交于不同的两点
交于不同的两点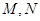 ,求
,求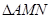 面积的取值范围.
面积的取值范围.
已知△ABC的顶点A(1,2)、B(-1,-1),直线l:2x+y-1=0是△ABC的一个内角平分线,求BC边所在直线的方程及点C到AB的距离.
下面三条直线l1:4x+y=4,l2:mx+y=0,l3:2x-3my=4不能构成三角形.求m的取值范围.
求经过直线3x-2y+1=0和x+3y+4=0的交点,且垂直于直线x+3y+4=0的直线l的方程.
过点M(0,1)作直线,使它被两已知直线l1:x-3y+10=0和l2:2x+y-8=0所截得的线段恰好被M所平分,求此直线方程.
已知过点A(1,1)且斜率为-m(m>0)的直线l与x、y轴分别交于P、Q两点,过P、Q两点作直线2x+y=0的垂线,垂足为R、S,求四边形PRSQ的面积的最小值.