“嫦娥三号”在距月球表面高度为H的轨道上绕月球作匀速圆周运动，测得此时的周期为
。之后经减速变轨下降到距离月表面h高度时，着陆器悬停在空中(此位置速度可视为0)，关闭反推发动机，着陆器以自由落体方式降落，在月球表面预选区将腿部支架扎进月球土层，成功实现软着陆。已知月球的半径为R,引力常为G.试求：
(1)月球的质量； (2)“嫦娥三号”关闭发动机后自由下落的时间。
）如图所示为一简易火灾报警装置.其原理是：竖直放置的试管中装有水银，当温度升高时，水银柱上升，使电路导通，蜂鸣器发出报警的响声.27℃时，空气柱长度L1为20cm，水银上表面与导线下端的距离L2为10cm，管内水银柱的高度h为13cm，大气压强P0=75cmHg.
（1）当温度达到多少摄氏度时，报警器会报警？
（2）如果要使该装置在87℃时报警，则应该再往玻璃管内注入多少cm高的水银柱？
如图所示，一个物块A（可看成质点）放在足够长的平板小车B的右端，A、B一起以v0的水平初速度沿光滑水平面向左滑行．左边有一固定的竖直墙壁，小车B与墙壁相碰，碰撞时间极短，且碰撞前、后无动能损失．已知物块A与小车B的水平上表面间的动摩擦因数为μ，重力加速度为g．
（1）若A、B的质量均为m，求小车与墙壁碰撞后的运动过程中，物块A所受摩擦力的冲量大小和方向；
（2）若A、B的质量比为k,且k＜1，求物块A在小车B上发生相对运动的过程中物块A对地的位移大小；
（3）若A、B的质量比为k，且k=2，求小车第一次与墙壁碰撞后的运动过程所经历的总时间．
如图所示，若电子由阴极飞出时的初速度忽略不计，电子发射装置的加速电压为U0.电容器板长和板间距离均为L＝10 cm，下极板接地．电容器右端到荧光屏的距离也是L＝10 cm.在电容器两极板间接一交变电压，上极板的电势随时间变化的图象如图所示．每个电子穿过两极板的时间极短，可以认为电压是不变的，求：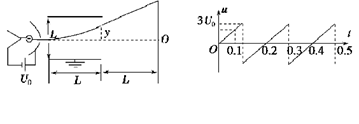
(1)在t＝0.06 s时刻，电子打在荧光屏上的何处？
(2)荧光屏上有电子打到的区间有多长？
(3)屏上的亮点如何移动？
如图所示，质量为m的小物块放在长直水平面上，用水平细线紧绕在半径为R、质量为2m的薄壁圆筒上．t=0时刻，圆筒在电动机带动下由静止开始绕竖直中心轴转动，转动中角速度满足ω=βt（β为已知常数），物块和地面之间动摩擦因数为μ．求：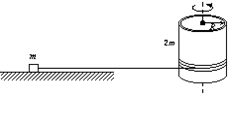
（1）物块运动中受到的拉力．（2）从开始运动至t=t1时刻，电动机对物块做了多少功？
如图所示，一质量M=3kg的足够长木板B静止于光滑水平面上，B的右边放有竖直挡板，B的右端距挡板S=4m。现有一小物体A（可视为质点）质量m=1kg，以速度v0=8m/s从B的左端水平滑上B，已知A和B 间的动摩擦因数μ=0.2，B与竖直挡板的碰撞时间极短，且碰撞时无机械能损失。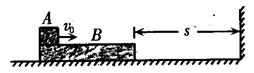
求：（1）B与竖直挡板碰撞前的速度是多少？
（2）若题干中的S可以任意改变（S不能为零）大小，要使B第一次碰墙后，AB系统动量为零，S的大小是多少？
（3）若要求B与墙碰撞两次，B的右端距挡板S应该满足什么条件？