已知函数f(x)=x2+2x+a.
(1)当a=
时,求不等式f(x)>1的解集.
(2)若对于任意x∈[1,+∞),f(x)>0恒成立,求实数a的取值范围.
已知a,b,c,d∈R,用分析法证明：ac+bd≤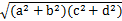
并指明等号何时成立.
已知等比数列{an}满足an+1+an=9·2n-1,n∈N*.
(1)求数列{an}的通项公式.
(2)设数列{an}的前n项和为Sn,若不等式Sn>kan-2对一切n∈N*恒成立,求实数k的取值范围.
已知首项为
的等比数列{an}的前n项和为Sn(n∈N*),且-2S2,S3,4S4成等差数列.
(1)求数列{an}的通项公式.
(2)证明Sn+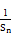
≤
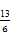(n∈N*).
已知数列{an}为等差数列,a3=5,a7=13,数列{bn}的前n项和为Sn,且有Sn=2bn-1,
(1)求{an},{bn}的通项公式.
(2)若cn=anbn,{cn}的前n项和为Tn,求Tn.
的部分图象如图所示.
的解析式，并写出
的内角分别是A，B，C，若
的值.