设等差数列{an}的首项a1为a,公差d=2,前n项和为Sn.
(1) 若当n=10时,Sn取到最小值,求 的取值范围;
的取值范围;
(2) 证明: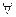 n∈N*, Sn,Sn+1,Sn+2不构成等比数列.
n∈N*, Sn,Sn+1,Sn+2不构成等比数列.
已知函数f ( )=
)=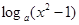 , 若
, 若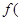 2)=1;
2)=1;
(1) 求a的值; (2)解不等式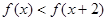 .
.
(本小题满分12分)已知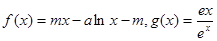 ,其中
,其中 均为实数,
均为实数,
(Ⅰ)求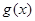 的极值;
的极值;
(Ⅱ)设 ,
,
求证:对 恒成立;
恒成立;
(Ⅲ)设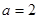 ,若对
,若对 给定的
给定的 ,在区间
,在区间 上总存在
上总存在 使得
使得 成立,求m的取值范围.
成立,求m的取值范围.
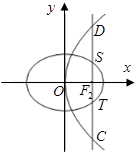
(本小题满分12分)如图,椭圆的右焦点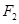 与抛物线
与抛物线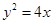 的焦点重合,过
的焦点重合,过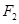 且于x轴垂直的直线与椭圆交于S,T,与抛物线交于C,D两点,且
且于x轴垂直的直线与椭圆交于S,T,与抛物线交于C,D两点,且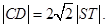
(Ⅰ)求椭圆的标准方程;
(Ⅱ)设P为椭圆上一点,若过点M(2,0)的直线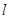 与椭圆相交于不同两点A和B,且满足
与椭圆相交于不同两点A和B,且满足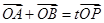 (O为坐标原点),求实数t的取值范围.
(O为坐标原点),求实数t的取值范围.
(本小题满分12分)已知E是矩形ABCD(如图1)边CD上的一点,现沿AE将△DAE折起至△D1AE(如图2),并且平面D1AE⊥平面ABCE,图3为四棱锥D1—ABCE的主视图与左视图.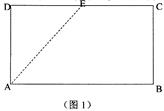

(Ⅰ)求证:直线BE⊥平面D1AE;
(Ⅱ)求点A到平面D1BC的距离.
(本小题满分12分)已知数列 的前
的前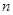 项和为
项和为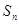 ,向量
,向量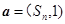 ,
, ,满足条件
,满足条件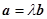 ,
, 且
且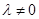 .
.
(Ⅰ)求数列 的通项公式;
的通项公式;
(Ⅱ)设函数 ,数列
,数列 满足条件
满足条件 ,
,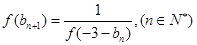
①求数列 的通项公式;
的通项公式;
②设 ,求数列
,求数列 的前
的前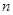 和
和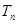 .
.