电视台为某个广告公司特约播放甲、乙两部电视连续剧．经调查，播放甲连续剧平均每集有收视观众20万人次，播放乙连续剧平均每集有收视观众15万人次，公司要求电视台每周共播放7集．
（1）设一周内甲连续剧播放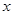
集，甲、乙两部连续剧的收视观众的人次的总和为
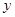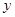万人次，求关于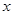的函数关系式；
（2）已知电视台每周只能为该公司提供不超过300分钟的播放时间，并且播放甲连续剧每集需要50分钟，播放乙连续剧每集需要35分钟，请你用所学知识求电视台每周应播放甲、乙两部连续剧各多少集，才能使得每周收看甲、乙连续剧的观众的人次总和最大，并求出这个最大值．
解分式方程：
．
先化简：
，再选择一个恰当的x值代入并求值．
计算：
．
已知：如图，抛物线
与
轴交于点
，与
轴交于点A、B，点A的坐标为（4，0）
求该抛物线的解析式；
点Q是线段AB上的动点，过点Q作QE//AC，交BC于点E，连接CQ，设△CQE的面积为S，Q(m，0)，试求S与m之间的函数关系式（写出自变量m的取值范围）；
在（2）的条件下，当△CQE的面积最大时，求点E的坐标.
若平行于x轴的动直线l与该抛物线交于点P，与直线AC交于点F，点D的坐标为(2，0). 问：是否存在这样的直线l，使得△ODF是等腰三角形？若存在，请求出点P的坐标，若不存在，请说明理由.
某瓜果基地市场部为指导该基地某种蔬菜的生产销售，在对历年市场行情和生产情况进行调查的基础上，对今年这种蔬菜上市后的市场售价和生产成本进行了预测，提供了两个方面的信息，如图（注：两图中的每个实心点所对应的纵坐标分别指相应月份的售价和成本，生产成本6月份最低，图甲的图象是直线，图乙的图象是抛物线）
请你根据图象提供的信息，解答下列问题：在3月份出售这种蔬菜，每千克的收益是多少元？（收益=售价－成本）
哪个月出售这种蔬菜，每千克的收益最大？说明理由.
已知市场部销售该种蔬菜，4，5两个月的总收益为48万元，且5月份的销量比4月份的销量多2万千克，求4，5两个月销量各多少万千克？
