已知函数 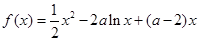 ,
, .
.
(1)当 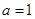 时,求函数
时,求函数  的最小值;
的最小值;
(2)当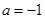 时,求证:无论
时,求证:无论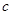 取何值,直线
取何值,直线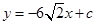 均不可能与函数
均不可能与函数 相切;
相切;
(3)是否存在实数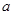 ,对任意的
,对任意的  ,且
,且 ,有
,有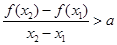 恒成立,若存在求出
恒成立,若存在求出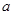 的取值范围,若不存在,说明理由。
的取值范围,若不存在,说明理由。
在△ABC中,角A、B、C的对边分别为a、b、c,向量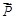 =(sinA,b+c),
=(sinA,b+c),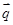 =(a-c,sinC-sinB),满足
=(a-c,sinC-sinB),满足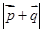 =
=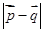
(Ⅰ)求角B的大小;
(Ⅱ)设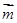 =(sin(C+
=(sin(C+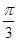 ),
),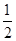 ),
), 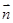 =(2k,cos2A) (k>1),
=(2k,cos2A) (k>1),  有最大值为3,求k的值.
有最大值为3,求k的值.
已知函数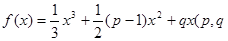 为常数)
为常数)
(1)若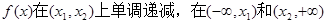 上单调递增,且
上单调递增,且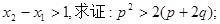
(2)若f(x)在x=1和x=3处取得极值,且在x∈[-6,6]时,函数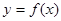 的图象在直线
的图象在直线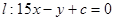
的下方,求c的取值范围.
(14分)如图所示,将一矩形花坛ABCD扩建成一个更大的矩形花园AMPN,要求B在AM上,D在AN上,且对角线MN过C点,已知|AB|=3米,|AD|=2米,
(1)要使矩形AMPN的面积大于32平方米,则AN的长应在什么范围内?
(2)当AN的长度是多少时,矩形AMPN的面积最小?并求出最小面积.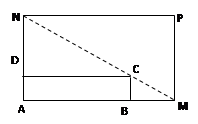
(本题18 分)已知数列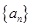 :
: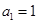 、
、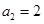 、
、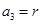 且
且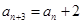 (
(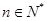 ),与数列
),与数列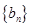 :
: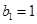 、
、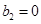 、
、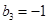 、
、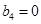 且
且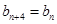 (
(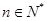 ).
).
记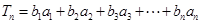 .
.
(1)若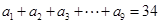 ,求
,求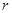 的值;
的值;
(2)求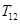 的值,并求证当
的值,并求证当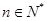 时,
时,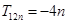 ;
;
(3)已知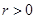 ,且存在正整数
,且存在正整数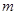 ,使得在
,使得在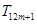 ,
,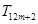 ,
, ,
,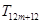 中有4项为100.求
中有4项为100.求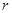 的值,并指出哪4项为100.
的值,并指出哪4项为100.
一台机器使用的时间较长,但还可以使用,它按不同的转速生产出来的某机械零件有一些会有缺点,每小时生产有缺点零件的多少,随机器的运转的速度而变化,下表为抽样试验的结果:
| 转速x(转/秒) |
2 |
4 |
5 |
6 |
8 |
| 每小时生产有缺点的零件数y(件) |
30 |
40 |
60 |
50 |
70 |
(1)画散点图
(2)如果y对x有线性相关关系,求回归直线方程;
(3)若实际生产中,允许每小时的产品中有缺点的零件最多为89个,那么机器的运转速度应控制在什么范围内?(参考数值: ,
, )
)