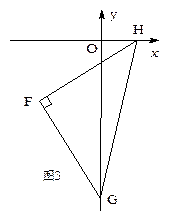如图,在直角坐标系xOy中,正方形OCBA的顶点A,C分别在y轴,x轴上,点B坐标为(6,6),抛物线y=ax2+bx+c经过点A,B两点,且3a-b=-1.
(1)求a,b,c的值;
(2)如果动点E,F同时分别从点A,点B出发,分别沿A→B,B→C运动,速度都是每秒1个单位长度,当点E到达终点B时,点E,F随之停止运动,设运动时间为t秒,△EBF的面积为S.
①试求出S与t之间的函数关系式,并求出S的最大值;
②当S取得最大值时,在抛物线上是否存在点R,使得以E,B,R,F为顶点的四边形是平行四边形?如果存在,求出点R的坐标;如果不存在,请说明理由.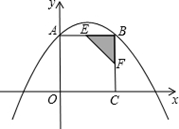
如图,有两个 的网格,网格中每个小正方形的边长均为1,每个网格中各画有一个梯形.请在图1、图2中分别画出一条线段,同时满足以下要求:
的网格,网格中每个小正方形的边长均为1,每个网格中各画有一个梯形.请在图1、图2中分别画出一条线段,同时满足以下要求:
(1)线段的一个端点为梯形的顶点,另一个端点在梯形一边的格点上;
(2)将梯形分成两个图形,其中一个是轴对称图形;
(3)图1、图2中分成的轴对称图形不全等.
分解因式:(1) ;(2)
;(2) .
.
先化简,再求值: ,其中
,其中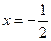
已知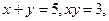 则
则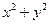 =""
=""
(1)如图,OA=2, P为y轴负半轴上一个动点,当P点沿y轴负半轴向下运动时,以P为顶点,PA为腰作等腰Rt△APD,过D作DE⊥x轴于E点,求OP-DE的值.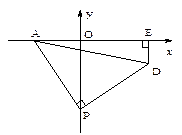
(2)如图,已知点F坐标为(-2,-2),当G在y轴的负半轴上沿负方向运动时,作Rt△FGH,始终保持∠GFH=90°,FG与y轴负半轴交于点G(0,m),FH与x轴正半轴交于点H(n,0),当G点在y轴的负半轴上沿负方向运动时,以下两个结论:①m—n为定值;②m+n为定值,其中只有一个结论是正确的,请找出正确的结论,并求出其值.