已知抛物线
，
（1）若
求该抛物线与x轴的交点坐标；
（2）若
，证明抛物线与x轴有两个交点；
（3）若
且抛物线在
区间上的最小值是-3，求b的值.
如图，有三条公路a，b，c，为了方便司机休息，路政部门确定修建一个休息站P，使它到三条公路的距离相等．（请用尺规作图，保留作图痕迹，不写作法．）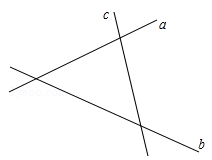
如图，∠1=∠2，∠C=∠D，AC与BD相交于点E，求证：CE=DE．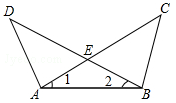
解分式方程：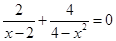
．
在平行四边形ABCD中，对角线AC和BD交于点O，AC=8．
（1）如图1，若AB⊥AC，BD=12，点P是线段AD上的动点（不包含端点A，D），过点P作PE⊥AC，垂足为点E，PF⊥BD，垂足为点F，设PE=x，PF=y，求y与x的函数关系式并直接写出自变量x的取值范围；
（2）如图2，若AE平分∠BAC，点F为BC中点，且点F保持在点E的右边，求线段BC的变化范围．
在平面直角坐标系中，直线y1=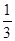
x+a和y2=﹣
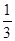x+b交于点E（3，3），点P（m，n）在直线y1=x+a上，过点P（m，n）作x轴的垂线，交直线y2=﹣x+b于点F．
（1）若n=2，求△PEF的面积；
（2）若PF=2，求点P的坐标．