在平面直角坐标系中，直线y1=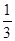
x+a和y2=﹣
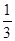x+b交于点E（3，3），点P（m，n）在直线y1=x+a上，过点P（m，n）作x轴的垂线，交直线y2=﹣x+b于点F．
（1）若n=2，求△PEF的面积；
（2）若PF=2，求点P的坐标．
如图所示的方格地面上，标有编号1、2、3的3个小方格地面是空地，另外6个方格地面是草坪，除此以外小方格地面完全相同.
（1）一只自由飞行的小鸟，将随意落在图中所示的方格地面上，求小鸟落在草坪上的概率；
（2）现准备从图中所示的3个小方格空地中任选2个种植草坪，则编号为1、2的2个小方格空地种植草坪的概率是多少（用树状图或列表法求解）？
从3名男生和2名女生中随机抽取2014年南京青奥会志愿者．求下列事件的概率：
（1）抽取1名，恰好是女生的概率；
（2）抽取2名，恰好是1名男生和1名女生．
（本题满分8）已知关于x的方程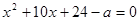
．
（1）若此方程有两个不相等的实数根，求a的范围；
（2）在（1）的条件下，当a取满足条件的最小整数，求此时方程的解．
解方程
（1）
（2）
中国移动开设两种通信业务如下（均指本地通话）：“全球通” 用户每月交纳50元月租费，然后按每分钟通话收费0．4元；另一种：“神州行”用户不用交纳租费 ，但每分钟通话收费0．6元，若一个月通话m分钟，“全球通” 用户的费用为X元，“神州行” 用户的费用为Y元，
（1）试用含m的代数式表示X和Y 。
（2）如果某人一个月通话6个小时，那么应选择哪种通话方式比较划算．