已知椭圆C的对称中心为原点O,焦点在x轴上,左右焦点分别为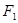 和
和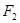 ,且|
,且|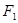
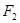 |=2,点(1,
|=2,点(1,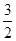 )在该椭圆上.
)在该椭圆上.
(1)求椭圆C的方程;
(2)过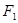 的直线
的直线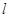 与椭圆C相交于A,B两点,以
与椭圆C相交于A,B两点,以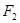 为圆心
为圆心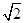 为半径的圆与直线
为半径的圆与直线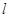 相切,求
相切,求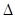 A
A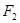 B的面积.
B的面积.
设数列{an}的前n项和为Sn=2n2,{bn}为等比数列,且a1=b1,b2(a2-a1)=b1.
(1)求数列{an}和{bn}的通项公式;
(2)设cn=,求数列{cn}的前n项和Tn.
本题满分12分)
一批救灾物资随26辆汽车从某市以x km/h的速度匀速开往相距400 km的灾区.为安全起见,每两辆汽车的前后间距不得小于 km,车速不能超过100km/h,设从第一辆汽车出发开始到最后一辆汽车到达为止这段时间为运输时
km,车速不能超过100km/h,设从第一辆汽车出发开始到最后一辆汽车到达为止这段时间为运输时 间,问运输时间最少需要多少小时?
间,问运输时间最少需要多少小时?
已知不等式x2-2x-3<0的解集为A,不等式x2+4x-5<0的解集为B,
(1)求A∪B;
(2)若不等式x2+ax+b<0的解集是A∪B,求ax2+x+b<0的解集
已知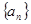 为等差数列,且
为等差数列,且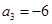 ,
,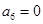
(1)求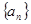 的通项公式;
的通项公式;
(2)若等差数列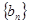 满足
满足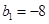 ,
,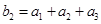 ,求
,求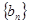 的前n项和.
的前n项和.
 在△ABC
在△ABC 中,已知
中,已知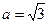 ,
,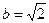 ,B=45°, 求A、C及c
,B=45°, 求A、C及c