在△ABC中,内角A,B,C的对边分别是a,b,c,且a2=b2+c2+ ab.
ab.
(1)求A.
(2)设a= ,S为△ABC的面积,求S+3cosBcosC的最大值,并指出此时B的值.
,S为△ABC的面积,求S+3cosBcosC的最大值,并指出此时B的值.
如图是某三棱柱被削去一个底面后的直观图与侧(左)视图、俯视图.已知CF=2AD,侧(左)视图是边长为2的等边三角形;俯视图是直角梯形,有关数据如图所示.求该几何体的体积.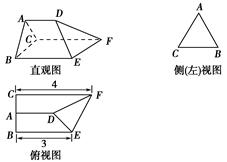
有一个倒圆锥形容器,它的轴截面是一个正三角形,在容器内放一个半径为r的铁球,并注入水,使水面与球正好相切,然后将球取出,求这时容器中水的深度.
如图所示是一几何体的直观图、正(主)视图、侧(左)视图、俯视图.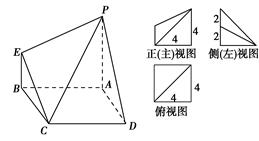
(1)若F为PD的中点,求证:AF⊥面PCD;
(2)求几何体BEC-APD的体积.
设数列{an}的前n项和为Sn,已知a1=1, =an+1-
=an+1-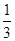 n2-n-
n2-n- ,n∈N*.
,n∈N*.
(1)求a2的值;
(2)求数列{an}的通项公式;
(3)证明:对一切正整数n,有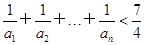 .
.
已知等差数列{an}满足a2=0,a6+a8=-10.
(1)求数列{an}的通项公式;
(2)求数列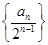 的前n项和.
的前n项和.