某中学为研究学生的身体素质与课外体育锻炼时间的关系,对400名高一学生的一周课外体育锻炼时间进行调查,结果如下表所示：

锻炼时间 (分钟)	[0,20)	[20,40)	[40,60)	[60,80)	[80,100)	[100,120)
人数	40	60	80	100	80	40

现采用分层抽样的方法抽取容量为20的样本.
(1)其中课外体育锻炼时间在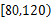分钟内的学生应抽取多少人?
(2)若从(1)中被抽取的学生中随机抽取2名,求这2名学生课外体育锻炼时间均在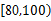分钟内的概率.

科目 数学   题型 解答题   难度 中等

知识点： 随机抽样