已知 是复数,
是复数,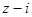 和
和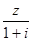 均为实数.
均为实数.
(1)求复数 ;
;
(2)若复数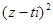 在复平面内对应点在第一象限,求实数t的取值范围.
在复平面内对应点在第一象限,求实数t的取值范围.
平面直角坐标系
中,已知椭圆
的离心率为
,左、右焦点分别是
,以
为圆心以3为半径的圆与以
为圆心以1为半径的圆相交,且交点在椭圆
上.
(Ⅰ)求椭圆
的方程;
(Ⅱ)设椭圆
,
为椭圆
上任意一点,过点
的直线
交椭圆
于
两点,射线
交椭圆
于点
.
(i)求
的值;
(Ⅱ)求
面积的最大值.
若
是一个三位正整数,且
的个位数字大于十位数字,十位数字大于百位数字,则称
为"三位递增数"(如137,359,567等).在某次数学趣味活动中,每位参加者需从所有的"三位递增数"中随机抽取1个数,且只能抽取一次.得分规则如下:若抽取的"三位递增数"的三个数字之积不能被5整除,参加者得0分;若能被5整除,但不能被10整除,得-1分;若能被10整除,得1分.
(Ⅰ)写出所有个位数字是5的"三位递增数" ;
(Ⅱ)若甲参加活动,求甲得分
的分布列和数学期望
.
设数列
的前
项和为
.已知
.
(Ⅰ)求
的通项公式;
(Ⅱ)若数列
满足
,求
的前
项和
.
如图,在三棱台
中,
分别为
的中点.
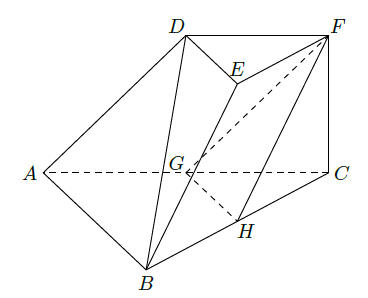
(Ⅰ)求证:
平面
;
(Ⅱ)若
平面
,
,
,求平面
与平面
所成的角(锐角)的大小.
设
.
(Ⅰ)求
的单调区间;
(Ⅱ)在锐角
中,角
的对边分别为
,若
,求
面积的最大值.