某村庄拟修建一个无盖的圆柱形蓄水池(不计厚度).设该蓄水池的底面半径为米,高为米,体积为立方米.假设建造成本仅与表面积有关,侧面积的建造成本为100元/平方米,底面的建造成本为160元/平方米,该蓄水池的总建造成本为12000元(π为圆周率).
(1)将表示成的函数,并求该函数的定义域;
(2)讨论函数的单调性,并确定和为何值时该蓄水池的体积最大.
(本小题满分13分)
设数列 的前
的前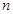 项和为
项和为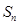 ,点
,点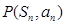 在直线
在直线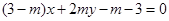 上,(
上,( 为常数,
为常数, ,
, ).
).
(1)求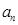 ;
;
(2)若数列 的公比
的公比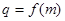 ,数列
,数列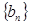 满足
满足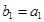 ,
, ,
,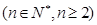 ,求证:
,求证: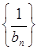 为等差数列,并求
为等差数列,并求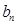 ;
;
(3)设数列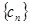 满足
满足 ,
, 为数列
为数列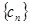 的前
的前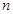 项和,且存在实数
项和,且存在实数 满足
满足
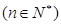 ,求
,求 的最大值.
的最大值.
(本小题满分12分)
将10个白小球中的3个染成红色,3个染成黄色,试解决下列问题:
求取出3个小球中红球个数 的分布列和数学期望;
的分布列和数学期望;
求取出3个小球中红球个数多于白球个数的概率.
本小题满分12分)
如图,正方形ABCD、ABEF的边长都是1,而且平面ABCD、ABEF互相垂直,点M在AC上移动,点N在BF上移动,若CM=BN=a(0<a<).
(1)求MN的长;
(2)当a为何值时,MN的长最小;
(3)当MN的长最小时,求面MNA与面MNB所成的二面角的余弦值.
(本小题满分12分)
在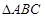 中,已知
中,已知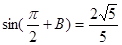 ,
,
(1) 求 的值;
的值;
(2) 若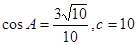 ,求
,求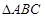 的面积;
的面积;
(3) 若函数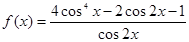 ,求
,求 的值.
的值.
(本小题满分14分)
已知函数 .
.
⑴若 ,求曲线
,求曲线 在点
在点 处的切线方程;
处的切线方程;
⑵若函数 在其定义域内为增函数,求正实数
在其定义域内为增函数,求正实数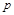 的取值范围;
的取值范围;
⑶设函数 ,若在
,若在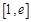 上至少存在一点
上至少存在一点 ,使得
,使得 成立,求实数
成立,求实数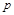 的取值范围.
的取值范围.