某学校组织了一次安全知识竞赛,现随机抽取20名学生的测试成绩,如下表所示(不低于90分的测试成绩称为“优秀成绩”):
| 79 |
90 |
82 |
80 |
84 |
95 |
79 |
86 |
89 |
91 |
| 97 |
86 |
79 |
78 |
86 |
77 |
87 |
89 |
83 |
85 |
(1)若从这20人中随机选取3人,求至多有1人是“优秀成绩”的概率;
(2)以这20人的样本数据来估计整个学校的总体数据,若从该校全体学生中(人数很多)任选3人,记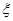 表示抽到“优秀成绩”学生的人数,求
表示抽到“优秀成绩”学生的人数,求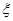 的分布列及数学期望.
的分布列及数学期望.
已知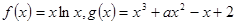
(1)如果函数 的单调递减区间为
的单调递减区间为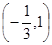 ,求函数
,求函数 的解析式;
的解析式;
(2)对一切的 ,
,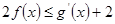 恒成立,求实数
恒成立,求实数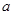 的取值范围.
的取值范围.
已知 ,
,
(1)求函数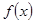 的单调区间;
的单调区间;
(2)求证:当 时,
时, .
.
若函数 ,当
,当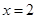 时,函数
时,函数 有极值-
有极值- .求函数
.求函数 的解析式.
的解析式.
命题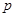 :关于
:关于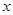 的不等式
的不等式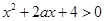 对一切
对一切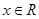 恒成立,
恒成立,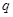 :函数
:函数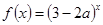 是增函数,若
是增函数,若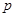 或
或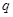 为真,
为真,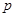 且
且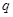 为假,求实数
为假,求实数 的取值范围.
的取值范围.
最近,李师傅一家三口就如何将手中的10万块钱投资理财,提出了三种方案:
第一种方案:李师傅的儿子认为:根据股市收益大的特点,应该将10万块钱全部用来买股票. 据分析预测:投资股市一年可能获利40%,也可能亏损20%(只有这两种可能),且获利与亏损的概率均为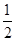 .
.
第二种方案:李师傅认为:现在股市风险大,基金风险较小,应将10万块钱全部用来买基金. 据分析预测:投资基金一年后可能获利20%,也可能损失10%,还可能不赔不赚,且这三种情况发生的概率分别为 ,
,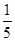 ,
,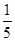 .
.
第三种方案:李师傅妻子认为:投入股市、基金均有风险,应该将10万块钱全部存入银行一年,现在存款年利率为4%,存款利息税率为5%.
针对以上三种投资方案,请你为李师傅家选择一种合理的理财方法,并说明理由.