设满足以下两个条件得有穷数列 为
为 阶“期待数列”:
阶“期待数列”:
① ,②
,② .
.
(1)若等比数列 为
为 阶“期待数列”,求公比
阶“期待数列”,求公比 ;
;
(2)若一个等差数列 既为
既为 阶“期待数列”又是递增数列,求该数列的通项公式;
阶“期待数列”又是递增数列,求该数列的通项公式;
(3)记 阶“期待数列”
阶“期待数列” 的前
的前 项和为
项和为 .
.
( )求证:
)求证: ;
;
(
 )若存在
)若存在 ,使
,使 ,试问数列
,试问数列
 是否为
是否为 阶“期待数列”?若能,求出所有这样的数列;若不能,请说明理由.
阶“期待数列”?若能,求出所有这样的数列;若不能,请说明理由.
数列 的前
的前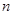 项和记为
项和记为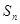 ,已知
,已知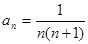 .
.
(Ⅰ)求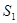 ,
,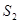 ,
,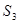 的值,猜想
的值,猜想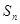 的表达式;
的表达式;
(Ⅱ)请用数学归纳法证明你的猜想.
已知极坐标的极点在平面直角坐标系的原点O处,极轴与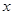 轴的正半轴重合,且长度单位相同.直线
轴的正半轴重合,且长度单位相同.直线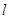 的极坐标方程为:
的极坐标方程为: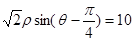 ,曲线C:
,曲线C: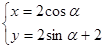 (
(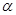 为参数),其中
为参数),其中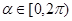 .
.
(Ⅰ)试写出直线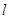 的直角坐标方程及曲线C的普通方程;
的直角坐标方程及曲线C的普通方程;
(Ⅱ)若点P为曲线C上的动点,求点P到直线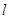 距离的最大值.
距离的最大值.
已知复数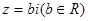 ,
,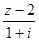 是实数,
是实数,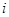 是虚数单位.
是虚数单位.
(1)求复数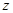 ;
;
(2)若复数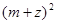 所表示的点在第一象限,求实数
所表示的点在第一象限,求实数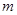 的取值范围.
的取值范围.
已知关于x的不等式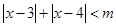 的解集不是空集.
的解集不是空集.
(1)求参数m的取值范围的集合M;
(2)设a,b M,求证:a+b<ab+1.
M,求证:a+b<ab+1.
已知曲线C的极坐标方程为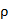 =2,以极点为原点,极轴为x轴的正半轴建立直角坐标系,P是曲线C上的动点,点A(2,0),M是线段AP的中点.
=2,以极点为原点,极轴为x轴的正半轴建立直角坐标系,P是曲线C上的动点,点A(2,0),M是线段AP的中点.
(1)求点M轨迹的直角坐标方程;
(2)求证:点M到点E( ,0)、F(3、0)的距离之比是常数.
,0)、F(3、0)的距离之比是常数.