已知中心在原点，焦点在轴上的椭圆的离心率为，椭圆上异于长轴顶-优题课

题文

已知中心在原点，焦点在轴上的椭圆的离心率为，椭圆上异于长轴顶点的任意点与左右两焦点、构成的三角形中面积的最大值为.
（1）求椭圆的标准方程；
（2）已知点，连接与椭圆的另一交点记为，若与椭圆相切时、不重合，连接与椭圆的另一交点记为，求的取值范围.

科目数学题型解答题难度中等

知识点：二次剩余

相关试题

（本小题满分14分）等比数列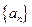中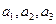，分别是下表第一、二、三行中的某一个数，且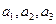中的任何两个数不在下表的同一列.

（Ⅰ）求数列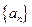的通项公式；
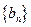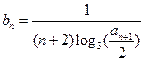（Ⅱ）若数列满足，记数列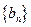的前n项和为，证明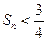

（本小题满分12分）如果直线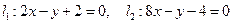与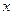轴正半轴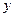，轴正半轴围成的四边形封闭区域（含边界）中的点，使函数的最大值为8，求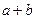的最小值

（本大题12分）已知二次函数．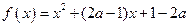
（1）判断命题：“对于任意的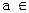R（R为实数集），方程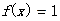必有实数根”的真假，并写出判断过程
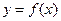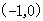（2），若在区间及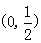内各有一个零点．求实数a的范围

（本小题满分14分已知函数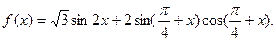
（I）化简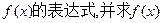的最小正周期；
（II）当的值域。

本小题满分14分)设函数且）
（1）求的单调区间；
（2）求的取值范围；
（3）已知对任意恒成立，求实数的取值范围。