某广告公司设计一个凸八边形的商标,它的中间是一个正方形,外面是四个腰长为 ,顶角为
,顶角为 的等腰三角形.
的等腰三角形.
(1)若角 时,求该八边形的面积;
时,求该八边形的面积;
(2)写出 的取值范围,当
的取值范围,当 取何值时该八边形的面积最大,并求出最大面积.
取何值时该八边形的面积最大,并求出最大面积.
如图,长方体 中,
中,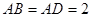 ,
,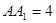 ,点
,点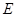 在
在 上,且
上,且 .
.
(Ⅰ)证明: 平面
平面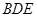 ;
;
(Ⅱ)求二面角 的余弦值.
的余弦值.
已知动点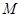 到
到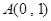 的距离比它到
的距离比它到 轴的距离多一个单位.
轴的距离多一个单位.
(Ⅰ)求动点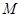 的轨迹
的轨迹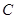 的方程;
的方程;
(Ⅱ)过点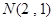 作曲线
作曲线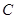 的切线
的切线 ,求切线
,求切线 的方程,并求出
的方程,并求出 与曲线
与曲线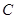 及
及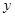 轴所围成图形的面积
轴所围成图形的面积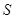 .
.
已知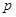 :“直线
:“直线 与圆
与圆 相交”;
相交”; :“方程
:“方程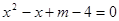 的两根异号”.若
的两根异号”.若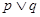 为真,
为真, 为真,求实数
为真,求实数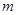 的取值范围.
的取值范围.
(本小题满分12分)
已知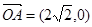 ,
, ,O为坐标原点,动点E满足:
,O为坐标原点,动点E满足:
(Ⅰ) 求点E的轨迹C的方程;
(Ⅱ)过曲线C上的动点P向圆O: 引两条切线PA、PB,切点分别为A、B,直线AB与x轴、y轴分别交于M、N两点,求ΔMON面积的最小值.
引两条切线PA、PB,切点分别为A、B,直线AB与x轴、y轴分别交于M、N两点,求ΔMON面积的最小值.
(本小题满分12分)
设函数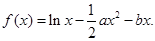
(Ⅰ) 当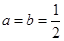 时,求函数
时,求函数 的最大值;
的最大值;
(Ⅱ)当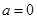 ,
,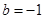 ,方程
,方程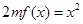 有唯一实数解,求正数
有唯一实数解,求正数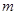 的值.
的值.