如图,在复平面内,复数 对应的向量分别是
对应的向量分别是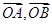 ,则
,则 ( )
( )
| A.2 | B.3 | C.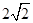 |
D. |
函数y=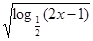 的定义域为()
的定义域为()
A.(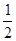 ,+∞) ,+∞) |
B.[1,+∞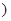 |
C.( 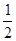 ,1 ,1 |
D.(-∞,1)) |
在棱长为 的正方体上,分别用过共顶点的三条棱中点的平面截该正方形,则截去
的正方体上,分别用过共顶点的三条棱中点的平面截该正方形,则截去 个三棱锥后 ,剩下的几何体的体积是()
个三棱锥后 ,剩下的几何体的体积是()
A. |
B.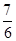 |
C.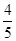 |
D. |
判断下列各组中的两个函数是同一函数的为()
(1) ,
,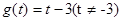 ;
;
(2) ,
, ;
;
(3) ,
, ;
;
(4) ,
,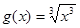 .
.
| A.(1),(4) | B.(2),(3) | C.(1) | D.(3) |
已知集合 则
则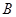 中所含元素个数为()
中所含元素个数为()
| A.3 | B.6 | C.8 | D.10 |
我国齐梁时代的数学家祖暅(公元前5-6世纪)提出了一条原理:“幂势既同,则积不容异.”这句话的意思是:夹在两个平行平面间的两个几何体,被平行于这两个平行平面的任何平面所截,如果截得的两个截面的面积总是相等,那么这两个几何体的体积相等.
设:由曲线 和直线
和直线 ,
,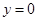 所围成的平面图形,绕
所围成的平面图形,绕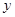 轴旋转一周所得到的旋转体为
轴旋转一周所得到的旋转体为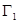 ;由同时满足
;由同时满足 ,
,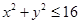 ,
, ,
, 的点
的点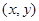 构成的平面图形,绕
构成的平面图形,绕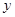 轴旋转一周所得到的旋转体为
轴旋转一周所得到的旋转体为 .根据祖暅原理等知识,通过考察
.根据祖暅原理等知识,通过考察 可以得到
可以得到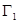 的体积为
的体积为
A. |
B.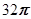 |
C. |
D.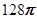 |