如图，直角梯形OABC中，AB∥OC，点A坐标为（0,6），点C坐标为（3,0），BC＝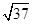
，一抛物线过点A、B、 C．
(1)填空：点B的坐标为 ；
(2)求该抛物线的解析式；
(3)作平行于x轴的直线与x轴上方的抛物线交于点E 、F，以EF为直径的圆恰好与x轴相切，求该圆的半径．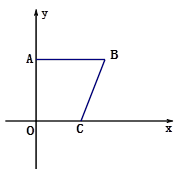
已知二次函数y=x2+bx+c中，函数y与自变量x的部分对应值如下表：
| x |
… |
-1 |
0 |
1 |
2 |
3 |
4 |
… |
| y |
… |
8 |
3 |
0 |
-1 |
0 |
3 |
… |
（1）求该二次函数的解析式；
（2）当x为何值时，y有最小值，最小值是多少？
（3）若A（m,y1）,B(m+2,y2)两点都在该函数的图象上，计算当m 取何值时，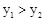
？
在平面直角坐标系xoy中，已知△ABC三个顶点的坐标分别为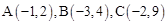
.
（1）画出△ABC；
（2）画出△ABC绕点A顺时针旋转
后得到的△AB1C1，并求出CC1的长.
如图，在△ABC中，点D在边AB上，满足且∠ACD=∠ABC，若AC=2，AD=1，求DB的长.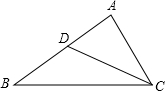
已知排水管的截面为如图所示的圆O,半径为10，圆心O到水面的距离是6，求水面宽AB.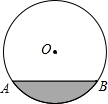
解方程：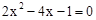
.