边长为2的正方形ABCD的两顶点A、C分别在正方形EFGH的两边DE、DG上(如图1)，现将正方形ABCD绕D点顺时针旋转，当A点第一次落在DF上时停止旋转，旋转过程中， AB边交DF于点M，BC边交DG于点N.
（1）求边DA在旋转过程中所扫过的面积；
（2）旋转过程中，当MN和AC平行时(如图2)，求正方形ABCD旋转的度数；
（3）如图3，设△MBN的周长为p，在旋转正方形ABCD的过程中，p值是否有变化？请证明你的结论.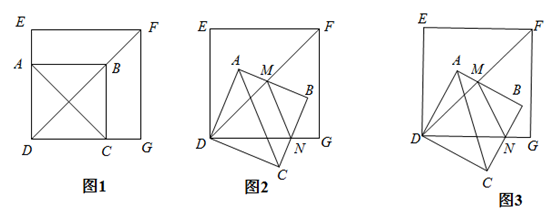
某企业500名员工参加安全生产知识测试，成绩记为A，B，C，D，E共5个等级，为了解本次测试的成绩（等级）情况，现从中随机抽取部分员工的成绩（等级），统计整理并制作了如下的统计图：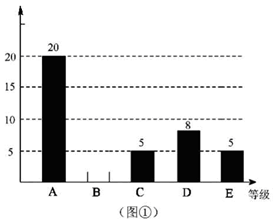
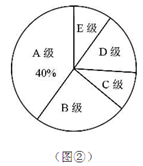
（1）求这次抽样调查的样本容量，并补全图①；
（2）如果测试成绩（等级）为A，B，C级的定为优秀，请估计该企业参加本次安全生产知识测试成绩（等级）达到优秀的员工的总人数．
苏州某旅行社组织甲、乙两个旅游团分别到西安、北京旅游．已知这两个旅游团共有55人，甲旅游团的人数比乙旅游团的人数的2倍少5人．问甲、乙两个旅游团各有多少人？
先化简，再求值：
，其中x＝
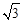－2．
解不等式组：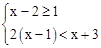
已知抛物线C1的顶点为P（1，0），且过点（0，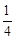
）．将抛物线C1向下平移h个单位（h＞0）得到抛物线C2．一条平行于x轴的直线与两条抛物线交于A、B、C、D四点（如图），且点A、C关于y轴对称，直线AB与x轴的距离是m2（m＞0）．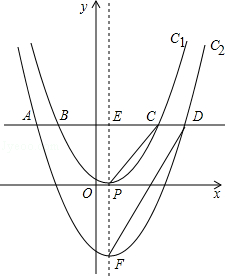
（1）求抛物线C1的解析式的一般形式；
（2）当m=2时，求h的值；
（3）若抛物线C1的对称轴与直线AB交于点E，与抛物线C2交于点F．求证：tan∠EDF﹣tan∠ECP=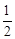
．