△ABC≌△DEF,且△ABC的周长为18.若AB等于5,EF等于6,求AC的值.
如图,△ABC中,∠ACB=90°,AC=6,BC=8.点P从A点出发沿A﹣C﹣B路径向终点运动,终点为B点;点Q从B点出发沿B﹣C﹣A路径向终点运动,终点为A点.点P和Q分别以1和3的运动速度同时开始运动,两点都要到相应的终点时才能停止运动,在某时刻,分别过P和Q作PE⊥l于E,QF⊥l于F.问:点P运动多少时间时,△PEC与QFC全等?请说明理由.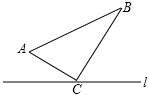
举反例说明下列命题是假命题.
(1)如果a+b>0,那么a>0,b>0;
(2)无限小数是无理数;
(3)两直线被第三条直线所截,同位角相等.
判断下列语句是不是命题,是命题,指出是真命题还是假命题.
(1)若一个数能被5整除,那么这个数也能被10整除;
(2)两个锐角的和是直角;
(3)同旁内角相等.
判断下列命题是真命题还是假命题,如果是假命题,举出一个反例.
(1)等角的余角相等;
(2)平行线的同旁内角的平分线互相垂直;
(3)和为180°的两个角叫做邻补角.