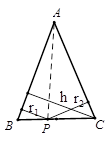
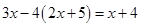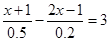阅读材料:如图,△ABC中,AB=AC,P为底边BC上任意一点,点P到两 腰的距离分别为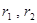 ,腰上的高为h,连结AP,则
,腰上的高为h,连结AP,则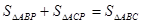 ,即:
,即: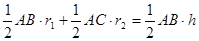 ,
,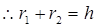 (1)理解与应用
(1)理解与应用
如果把“等腰三角形”改成“等边三角形”,那么P的位置可以由“在底边上任一点”放宽为“在 三角形内任一点”,即:已知边长为2的等边△ABC内任意一点P到各边的距离分别为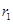 ,
,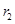 ,
,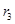 ,试证明:
,试证明: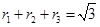 .
.
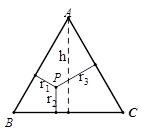
(2)类比与推理
边长为2的正方形内任意一点到各边的距离的和等于 ;
(3)拓展与延伸
若边长为2的正n边形A1A2…An内部任意一点P到各边的距离为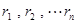 ,请问
,请问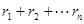 是否为定值(用含n的式子表示),如果是,请合理猜测出这个定值。
是否为定值(用含n的式子表示),如果是,请合理猜测出这个定值。
如图,一只甲虫在5×5的方格(每小格边长为1)上沿着网格线运动.它从A处出发去看望B、C、D处的其它甲虫,规定:向上向右走为正,向下向左走为负.如果从A到B记为:A→B(+1,+4),从B到A记为:B→A(-1,-4),其中第一个数表示左右方向,第二个数表示上下方向.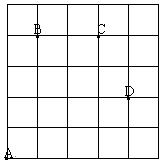
图中A→C(,),B→C(,),C→(+1,)
若这只甲虫从A处去甲虫P处的行走路线依次为(+2,+2),(+2,-1),
(-2,+3),(-1,-2),请在图中标出P的位置;若这只甲虫的行走路线为A→B→C→D,请计算该甲虫走过的路程.
若图中另有两个格点M、N,且M→A( 3-a, b-4),M→N( 5-a, b-2),则N→A应记为什么?
某人去水果批发市场采购苹果,他看中了A、B两家苹果。这两家苹果品质一样,零售价都为6元/千克,批发价各不相同。
A家规定:批发数量不超过1000千克,按零售价的92%优惠;批发数量不超过2000千克,按零售价的90%优惠;超过2000千克的按零售价的88%优惠。
B家的规定如下表:
【表格说明:批发价格分段计算,如:某人批发苹果2100千克,则总费用=6×95%×500+6×85%×1000+6×75%×(2100-1500)】如果他批发600千克苹果,则他在A家批发需要_____________元,在B家批发需要
_________元;如果他批发x千克苹果(1500<
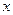 <2000),则他在A家批发需要__________元,在B 家批发需要________ 元(用含x的代数式表示)
<2000),则他在A家批发需要__________元,在B 家批发需要________ 元(用含x的代数式表示)现在他要批发1800千克苹果,你能帮助他选择在哪家批发更优惠吗?请说明理由。
某自行车厂计划一周生产自行车1400辆,平均每天生产200辆,但由于种种原因,实际每天生产量与计划量相比有出入.下表是某周的生产情况(超产记为正、减产记为负):
根据记录的数据可知该厂星期六生产自行车___________ __辆
根据记录的数据可知该厂本周实际生产自行车_____________辆;
产量最多的一天比产量最少的一天多生产自行车____________辆;
该厂实行每周计件工资制,每生产一辆车可得50元,若超额完成任务,则超过部分每辆另奖15元;少生产一辆扣20元,那么该厂工人这一周的工资总额是多少元?
若新规定这样一种运算法则:a※b=a2+2ab,例如3※(-2)=32+2×3×(-2)=-3试求(-2)※3的值
若1※x="3" , 求x的值
若(-2)※x=" -2+" x , 求x的值
解方程