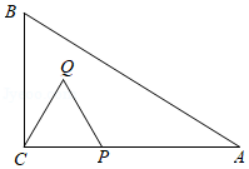
如图,在 中, , , .点 是 边上的一动点,点 从点 出发以每秒 的速度沿 方向匀速运动,以 为边作等边 (点 、点 在 同侧),设点 运动的时间为 秒, 与 重叠部分的面积为 .
(1)当点 落在 内部时,求此时 与 重叠部分的面积 (用含 的代数式表示,不要求写 的取值范围);
(2)当点 落在 上时,求此时 与 重叠部分的面积 的值;
(3)当点 落在 外部时,求此时 与 重叠部分的面积 (用含 的代数式表示).
已知:直线a∥b,点A、B在直线a上,点C、D在直线b上,如图
(1). 若 ,则
,则

(2). 若 ,那么
,那么 吗?说明你的理由。
吗?说明你的理由。
某单位欲招聘一名员工,现有 三人竞聘该职位,他们的笔试成绩和口试成绩(单位:分)分别用两种方式进行了统计,如表一和图一.
三人竞聘该职位,他们的笔试成绩和口试成绩(单位:分)分别用两种方式进行了统计,如表一和图一.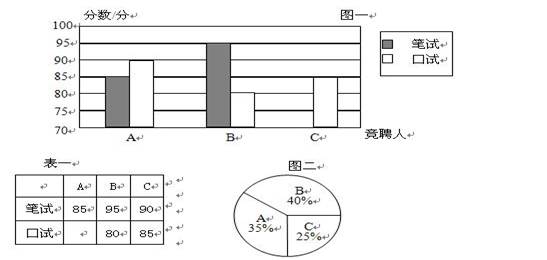
(1). 请将表一和图一中的空缺部分补充完整;
(2). 竞聘的最后一个程序是由该单位的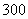 名职工进行投票,三位竞聘者的得票情
名职工进行投票,三位竞聘者的得票情
(3). 若每票计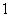 分,该单位将笔试、口试、得票三项测试得分按
分,该单位将笔试、口试、得票三项测试得分按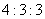 的比例确定 个人成绩,请计算三位竞聘者的最后成绩,并根据成绩判断谁能竞聘成功.
的比例确定 个人成绩,请计算三位竞聘者的最后成绩,并根据成绩判断谁能竞聘成功.
建设中的昆石高速公路,在某施工段上沿AC方向开山修路,为加快施工速度,要在山坡的另一边同时施工,如图所示,从AC上的一点B取∠ABD=150°,BD=380米,∠D=60°,那么开挖点E离D多远,正好使A、C、E成一直线.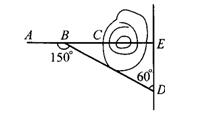
解不等式组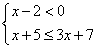 ;并写出它的整数解。
;并写出它的整数解。
已知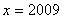 ,
,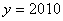 ,求代数式
,求代数式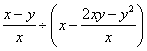 的值。
的值。