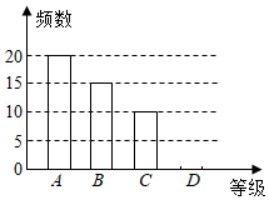
某校开展主题为"防疫常识知多少"的调查活动,抽取了部分学生进行调查,调查问卷设置了 :非常了解、 :比较了解、 :基本了解、 :不太了解四个等级,要求每个学生填且只能填其中的一个等级,采取随机抽样的方式,并根据调查结果绘制成如图所示不完整的频数分布表和频数分布直方图,根据以上信息回答下列问题:
等级 |
频数 |
频率 |
|
20 |
0.4 |
|
15 |
|
|
10 |
0.2 |
|
|
0.1 |
(1)频数分布表中 , ,将频数分布直方图补充完整;
(2)若该校有学生1000人,请根据抽样调查结果估算该校"非常了解"和"比较了解"防疫常识的学生共有多少人?
(3)在"非常了解"防疫常识的学生中,某班有5个学生,其中3男2女,计划在这5个学生中随机抽选两个加入防疫志愿者团队,请用列表或画树状图的方法求所选两个学生中至少有一个女生的概率.
已知:点O到△ABC的两边AB,AC所在直线的距离相等,且OB=OC.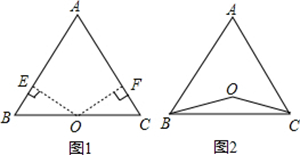
(1)如图1,若点O在边BC上,求证:AB=AC;
(2)如图2,若点O在△ABC的内部,求证:AB=AC;
(3)若点O在△ABC的外部,AB=AC成立吗?请画出图表示.
在Rt△ABC中,AC=3cm,AB=5cm,四边形CFDE为矩形,其中CF、CE在两直角边上.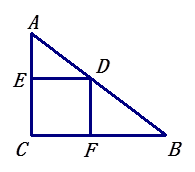
(1)求BC的长度.
(2)设矩形的一边CF=xcm.当矩形ECFD是3㎝2,求矩形的长和宽是多少?
将一条长为20cm的铁丝剪成两段,并以每一段铁丝的长度为周长做成一个正方形.
(1)要使这两个正方形的面积之和等于17cm2,那么这段铁丝剪成两段后的长度分别是多少?
(2)两个正方形的面积之和可能等于12cm2吗?若能,求出两段铁丝的长度;若不能,请说明理由.
如图,在Rt△ACB中,∠C=90°,BE平分∠ABC,ED垂直平分AB于D.若AC=9,求AE的值.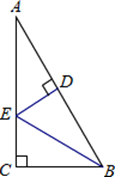
某商场将进货价为40元的台灯以50元售出,平均每月能售出600个,调查表明,售价在50~70元的范围内,这种台灯的售价每上涨2元,其销售量就减少20个,为了实现平均每月10000元的销售利润,这种台灯的售价应定为多少?这时应进台灯多少个?