每年的三月十二日，是中国的植树节，林管部门在植树前，为保证树苗的质量，都会在植树前对树苗进行检测.现从甲、乙两种树苗中各抽测了10株树苗的高度，规定高于128厘米的树苗为“良种树苗”，测得高度如下(单位：厘米)：
甲：137，121，131，120，129，119，132，123，125，133；
乙：110，130，147，127，146，114，126，110，144，146.
（1）根据抽测结果，画出甲、乙两种树苗高度的茎叶图，并根据你填写的茎叶图，对甲、乙两种树苗的高度作比较，写出对两种树苗高度的统计结论；
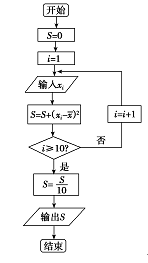
（2）设抽测的10株甲种树苗高度平均值为x，将这10株树苗的高度依次输入按程序框图进行运算(如图)，问输出的S大小为多少？并说明S的统计学意义；
（3）若小王在甲种树苗中随机领取了5株进行种植，用样本的频率分布估计总体分布，求小王领取到的“良种树苗”的株数X的分布列.
中，
, 沿平面
把这个长方体截成两个几何体: 几何体（1）；几何体（2）
、
，求
的正切值
，
，其中
且
.
，求
的值；（II） 若
，求
中，底面
为菱形，
平面
为
的中点，
平面
；（II）平面
⊥平面
.
的三个顶点为
.
所在的直线方程；（Ⅱ）求中线
所在直线的方程.
，
，求方程
的根；
满足
，求函数在
的值域．