(19分)如图甲所示，表面绝缘、倾角q=30°的斜面固定在水平地面上，斜面的顶端固定有弹性挡板，挡板垂直于斜面，并与斜面底边平行。斜面所在空间有一宽度D=0.40m的匀强磁场区域，其边界与斜面底边平行，磁场方向垂直斜面向上，磁场上边界到挡板的距离s=0.55m。一个质量m=0.10kg、总电阻R=0.25W的单匝矩形闭合金属框abcd，放在斜面的底端，其中ab边与斜面底边重合，ab边长L=0.50m。从t=0时刻开始，线框在垂直cd边沿斜面向上大小恒定的拉力作用下，从静止开始运动，当线框的ab边离开磁场区域时撤去拉力，线框继续向上运动，并与挡板发生碰撞，碰撞过程的时间可忽略不计，且没有机械能损失。线框向上运动过程中速度与时间的关系如图乙所示。已知线框在整个运动过程中始终未脱离斜面，且保持ab边与斜面底边平行，线框与斜面之间的动摩擦因数m=
/3，重力加速度g取10 m/s2。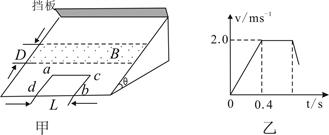
(1)求线框受到的拉力F的大小；
(2)求匀强磁场的磁感应强度B的大小；
(3)已知线框向下运动通过磁场区域过程中的速度v随位移x的变化规律满足v＝v0-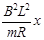
(式中v0为线框向下运动ab边刚进入磁场时的速度大小，x为线框ab边进入磁场后对磁场上边界的位移大小)，求线框在斜面上运动的整个过程中产生的焦耳热Q。
如图所示，真空中金属板M、N相距为d，当N板用波长为λ的光照射时，电路中的电流恒为I.设电子的电荷量为e，质量为m，真空中光速为c.
（1）求每秒到达M板的电子数.
（2）当垂直于纸面再加一匀强磁场，且磁感应强度为B时，电路中的电流恰好为零，求从N板逸出光电子的最大初动能和N板的逸出功.
如图12所示质量为M的小物块A静止在离地面高h的水平桌面的边缘，质量为m的小物块B沿桌面向A运动并以速度v0与之发生正碰（碰撞时间极短）。碰后A离开桌面，其落点离出发点的水平距离为L。碰后B反向运动。已知B与桌面的动摩擦因数为μ，重力加速度为g，桌面足够长。求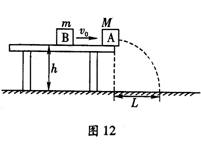
（1）碰后A、B小物块分离的瞬间速率各是多少？
（2）碰后小物块B后退的最大距离是多少？
一人用一根长L=1m，最大只能承受T=46N拉力的轻绳子，拴着一个质量m=1kg的小球（不考虑其大小），在竖直平面内作圆周运动，已知圆心O离地高H=21m，如图7所示，若小球运动到达最低点时绳刚好被球拉断，求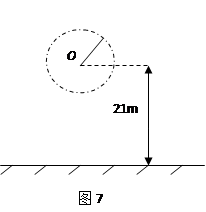
（1）小球到达最低点的速度大小是多少?
（2）小球落地点到O点的水平距离是多少?（g=10m/s2）
如图所示，在绕竖直轴匀速转动的水平圆盘盘面上，离轴心r = 20cm处放置一小物块A，其质量m = 2kg，试求：
（1）当圆盘转动的角速度ω = 2rad/s，转动一圈需要的时间是多少？物块A的速度是多少？
（2）A与盘面间的静摩擦力的最大值为其重力的0．5倍，若使A与盘面间不发生相对滑动，则圆盘转动的最大角速度是多大? （取g = 10m/s2）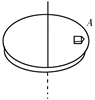
某人在离地高H="15" m的屋顶将手伸出屋檐,以初速度V0=10m/s竖直向上抛出一小球，不考虑空气阻力的影响，它抛出以后运动的过程中, 求：
（1）小球抛出后离地的最大高度是多少？
（2）小球经多长时间落到地上？
（3）小球落地的速度大小是多少？（g取10 m/s2）。