填写推理理由(1×10=10分)
如图,已知AB∥CD ,∠1=∠2,∠3=∠4,试说明AD∥BE
解:∵AB∥CD(已知)
∴∠4=∠_____( )
∵∠3=∠4(已知)
∴∠3=∠_____( )
∵∠1=∠2(已知)
∴∠ CAE+ =∠CAE+
即 ∠_____ =∠_____
∴∠3=∠_____
∴AD∥BE( )
如图,AB是半圆O的直径,C是AB延长线上的一点,CD与半圆O相切于点D,连接AD,BD.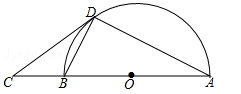
(1)求证:∠BAD=∠BDC;
(2)若∠BDC=28°,BD=2,求⊙O的半径.(精确到0.01)
如图, 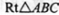 中,
中,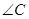 =900,AC=
=900,AC=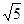 ,tanB=
,tanB=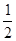 。半径为2的
。半径为2的 ,分别交AC,BC于点D,E,得到
,分别交AC,BC于点D,E,得到
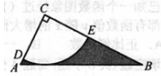
(1)求证, AB为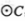 的切线:
的切线:
(2)求图中阴影部分的面积
已知四边形ABCD内接于⊙O,∠ADC=90°,∠DCB<90°,对角线AC平分∠DCB ,延长DA,CB相交于点E.
(1)如图1,EB=AD,求证:△ABE是等腰直角三角形;
(2)如图2,连接OE,过点E作直线EF,使得∠OEF=30°,当∠ACE≥30°时,判断直线EF与⊙O的位置关系,并说明理由.
如图,在矩形ABCD中,点E在边CD上,将该矩形沿AE折叠,使点D落在边BC上的点F处,过点F作分、FG∥CD,交AE于点G连接DG.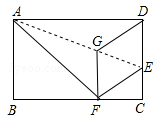
(1)求证:四边形DEFG为菱形;
(2)若CD=8,CF=4,求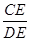 的值.
的值.
如图,在10×10的正方形网格中,点A,B,C,D均在格点上,以点A为位似中心画四边形AB′C′D′,使它与四边形ABCD位似,且相似比为2.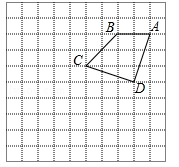
(1)在图中画出四边形AB′C′D′;
(2)填空:△AC′D′是 三角形.