小明在一次数学兴趣小组活动中，对一个数学问题作如下探究：
问题情境：如图1，四边形ABCD中，AD∥BC，点E为DC边的中点，连接AE并延长交BC的延长线于点F，求证：S四边形ABCD=S△ABF（S表示面积）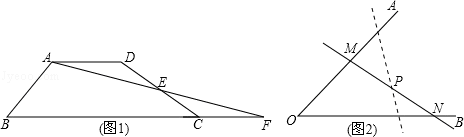
问题迁移：如图2：在已知锐角∠AOB内有一个定点P．过点P任意作一条直线MN，分别交射线OA、OB于点M、N．小明将直线MN绕着点P旋转的过程中发现，△MON的面积存在最小值，请问当直线MN在什么位置时，△MON的面积最小，并说明理由．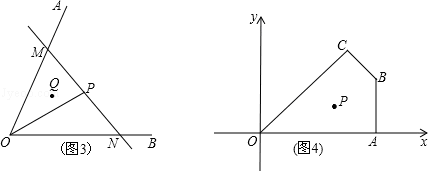
实际应用：如图3，若在道路OA、OB之间有一村庄Q发生疫情，防疫部门计划以公路OA、OB和经过防疫站P的一条直线MN为隔离线，建立一个面积最小的三角形隔离区△MON．若测得∠AOB=66°，∠POB=30°，OP=4km，试求△MON的面积．（结果精确到0.1km2）（参考数据：sin66°≈0.91，tan66°≈2.25，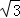
≈1.73）
拓展延伸：如图4，在平面直角坐标系中，O为坐标原点，点A、B、C、P的坐标分别为（6，0）（6，3）（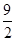
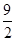，）、（4、2），过点p的直线l与四边形OABC一组对边相交，将四边形OABC分成两个四边形，求其中以点O为顶点的四边形面积的最大值．
已知，如图, DE⊥AC, ∠AGF=∠ABC, ∠1+∠2=1800,试判断BF与AC的位置关系, 并说明理由.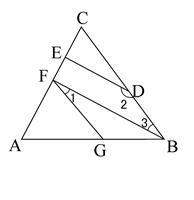
小龙在学校组织的社会调查活动中负责了解他所居住的小区500户居民的家庭收入情况。他从中随机调查了40户居民家庭的收入情况（收入取整数，单位：元），并绘制了如下的频数分布表和频数分布直方图。
根据以上提供的信息，解答下列问题：
（1）补全频数分布表；
（2）补全频数分布直方图；
（3）请你估计该居民小区家庭属于中等收入（大于或等于1000不足1600元）的大约有多少户？
| 分组 |
频数 |
百分比 |
| 600≤x＜800 |
2 |
5％ |
| 800≤x＜1000 |
6 |
15％ |
| 1000≤x＜1200 |
45％ |
|
| 1200≤x＜1400 |
9 |
22.5％ |
| 1400≤x＜1600 |
||
| 1600≤x＜1800 |
2 |
5％ |
| 合计 |
40 |
100％ |
（7分) 如图，平面直角坐标系中，已知点A（－3，3），B（－5，1），C（－2，0），P(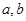
)是△ABC的边AC上任意一点，△ABC经过平移后得到△A1B1C1，已知点P的对应点为P1(
)．
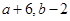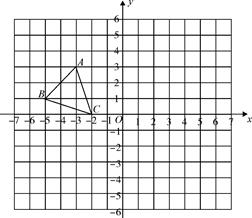
（1）直接写出点C1的坐标；
（2）在图中画出△A1B1C1；
（3）求△AOA1的面积．
下面是某同学给出一种证法，请你将解答中缺少的条件、结论或证明理由补充完整：
证明：
（已知）
(_________________________)
AB//CD(已知)
( _______________________）
是
的平分线，(已知)
_______(角平分线定义)
(已证)
（_________________）_______________________(已证)
(等量代换)
（1题5分、2题6分满分11分）
（1）解方程组
（2）解不等式组
并把它的解集在数轴上表示出来。