小龙在学校组织的社会调查活动中负责了解他所居住的小区500户居民的家庭收入情况。他从中随机调查了40户居民家庭的收入情况（收入取整数，单位：元），并绘制了如下的频数分布表和频数分布直方图。
根据以上提供的信息，解答下列问题：
（1）补全频数分布表；
（2）补全频数分布直方图；
（3）请你估计该居民小区家庭属于中等收入（大于或等于1000不足1600元）的大约有多少户？
| 分组 |
频数 |
百分比 |
| 600≤x＜800 |
2 |
5％ |
| 800≤x＜1000 |
6 |
15％ |
| 1000≤x＜1200 |
|
45％ |
| 1200≤x＜1400 |
9 |
22.5％ |
| 1400≤x＜1600 |
|
|
| 1600≤x＜1800 |
2 |
5％ |
| 合计 |
40 |
100％ |
如图，抛物线y=ax2+bx-4a经过A（-1，0）、C（0，4）两点，与x轴交于另一点B．
（1）求抛物线的解析式；
（2）已知点D（m，m+1）在第一象限的抛物线上，求点D关于直线BC对称的点的坐标；
（3）在（2）的条件下，连接BD，点P为抛物线上一点，且∠DBP=45°，求点P的坐标．
如图，点C是半圆O的半径OB上的动点，作PC⊥AB于C．点D是半圆上位于PC左侧的点，连接BD交线段PC于E，且PD=PE．
（1）求证：PD是⊙O的切线；
（2）若⊙O的半径为4
，PC=8，设OC=x，PD2=y．
①求y关于x的函数关系式；
②当x=时，求tanB的值．
我市某乡镇学校教学楼后面靠近一座山坡，坡面上是一块平地，如图所示，BC∥AD，斜坡AB=40米，坡角∠BAD=60°，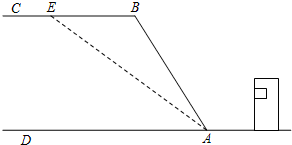
（1）求山坡高度；
（2）为防夏季因瀑雨引发山体滑坡，保障安全，学校决定对山坡进行改造，经地质人员勘测，当坡角不超过45°时，可确保山体不滑坡，改造时保持坡脚A不动，从坡顶B 沿BC削进到E处，问BE至少是多少米（结果保留根号）？
已知：如图所示，△ABC为任意三角形，若将△ABC绕点C顺时针旋转180° 得到△DEC．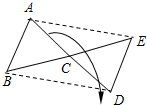
（1）试猜想AE与BD有何关系？并且直接写出答案．
（2）若△ABC的面积为4cm2，求四边形ABDE的面积；
（3）请给△ABC添加条件，使旋转得到的四边形ABDE为矩形，并说明理由．
甲、乙两公司各为“见义勇为基金会”捐款30 000元，已知乙公司比甲公司人均多捐20元，且甲公司的人数比乙公司的人数多20%．问甲、乙两公司各有多少人？