如图,点C是半圆O的半径OB上的动点,作PC⊥AB于C.点D是半圆上位于PC左侧的点,连接BD交线段PC于E,且PD=PE.
(1)求证:PD是⊙O的切线;
(2)若⊙O的半径为4 ,PC=8
,PC=8 ,设OC=x,PD2=y.
,设OC=x,PD2=y.
①求y关于x的函数关系式;
②当x= 时,求tanB的值.
时,求tanB的值.
如图,已知 是 的直径,点 是 上一点,连接 ,点 关于 的对称点 恰好落在 上.
(1)求证: ;
(2)过点 作 的切线 ,交 的延长线于点 .如果 , ,求 的直径.

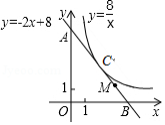
如图,已知一次函数 的图象与坐标轴交于 , 两点,并与反比例函数 的图象相切于点 .
(1)切点 的坐标是 ;
(2)若点 为线段 的中点,将一次函数 的图象向左平移 个单位后,点 和点 平移后的对应点同时落在另一个反比例函数 的图象上时,求 的值.
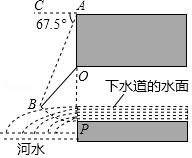
如图所示是我国古代城市用以滞洪或分洪系统的局部截面原理图,图中 为下水管道口直径, 为可绕转轴 自由转动的阀门.平时阀门被管道中排出的水冲开,可排出城市污水;当河水上涨时,阀门会因河水压迫而关闭,以防河水倒灌入城中.若阀门的直径 , 为检修时阀门开启的位置,且 .
(1)直接写出阀门被下水道的水冲开与被河水关闭过程中 的取值范围;
(2)为了观测水位,当下水道的水冲开阀门到达 位置时,在点 处测得俯角 ,若此时点 恰好与下水道的水平面齐平,求此时下水道内水的深度.(结果保留小数点后一位)
, , , , , ,
某文具店最近有 , 两款毕业纪念册比较畅销,近两周的销售情况是:第一周 款销售数量是15本, 款销售数量是10本,销售总价是230元;第二周 款销售数量是20本, 款销售数量是10本,销售总价是280元.
(1)求 , 两款毕业纪念册的销售单价;
(2)若某班准备用不超过529元购买这两种款式的毕业纪念册共60本,求最多能够买多少本 款毕业纪念册.
为落实立德树人的根本任务,加强思改、历史学科教师的专业化队伍建设.某校计划从前来应聘的思政专业(一名研究生,一名本科生)、历史专业(一名研究生、一名本科生)的高校毕业生中选聘教师,在政治思想审核合格的条件下,假设每位毕业生被录用的机会相等
(1)若从中只录用一人,恰好选到思政专业毕业生的概率是
(2)若从中录用两人,请用列表或画树状图的方法,求恰好选到的是一名思政研究生和一名历史本科生的概率.