如图,已知抛物线y=x2+bx+c经过A(-1,0)、B(4,5)两点,过点B作BC⊥x轴,垂足为C.
(1)求抛物线的解析式;
(2)求tan∠ABO的值;
(3)点M是抛物线上的一个点,直线MN平行于y轴交直线AB于N,如果以M、N、B、C为顶点的四边形是平行四边形,求出点M的横坐标.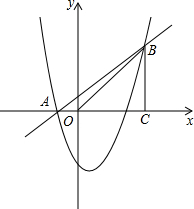
在美丽乡村建设中,某县政府投入专项资金,用于乡村沼气池和垃圾集中处理点建设.该县政府计划:2018年前5个月,新建沼气池和垃圾集中处理点共计50个,且沼气池的个数不低于垃圾集中处理点个数的4倍.
(1)按计划,2018年前5个月至少要修建多少个沼气池?
(2)到2018年5月底,该县按原计划刚好完成了任务,共花费资金78万元,且修建的沼气池个数恰好是原计划的最小值.据核算,前5个月,修建每个沼气池与垃圾集中处理点的平均费用之比为 .为加大美丽乡村建设的力度,政府计划加大投入,今年后7个月,在前5个月花费资金的基础上增加投入 ,全部用于沼气池和垃圾集中处理点建设.经测算:从今年6月起,修建每个沼气池与垃圾集中处理点的平均费用在2018年前5个月的基础上分别增加 , ,新建沼气池与垃圾集中处理点的个数将会在2018年前5个月的基础上分别增加 , ,求 的值.
如图,在平面直角坐标系中,直线 与直线 交点 的横坐标为2,将直线 沿 轴向下平移4个单位长度,得到直线 ,直线 与 轴交于点 ,与直线 交于点 ,点 的纵坐标为 .直线 与 轴交于点 .
(1)求直线 的解析式;
(2)求 的面积.

某学校开展以素质提升为主题的研学活动,推出了以下四个项目供学生选择: .模拟驾驶; .军事竞技; .家乡导游; .植物识别.学校规定:每个学生都必须报名且只能选择其中一个项目.八年级(3)班班主任刘老师对全班学生选择的项目情况进行了统计,并绘制了如下两幅不完整的统计图.请结合统计图中的信息,解决下列问题:
(1)八年级(3)班学生总人数是 ,并将条形统计图补充完整;
(2)刘老师发现报名参加“植物识别”的学生中恰好有两名男生,现准备从这些学生中任意挑选两名担任活动记录员,请用列表或画树状图的方法,求恰好选中1名男生和1名女生担任活动记录员的概率.

如图, , 的顶点 , 分别落在直线 , 上, 交 于点 , 平分 .若 , ,求 的度数.

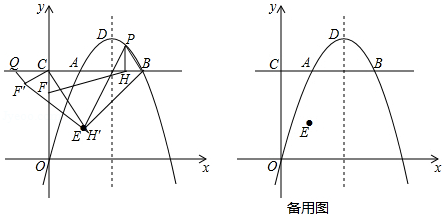
如图,在平面直角坐标系中,点 在抛物线 上,且横坐标为1,点 与点 关于抛物线的对称轴对称,直线 与 轴交于点 ,点 为抛物线的顶点,点 的坐标为 .
(1)求线段 的长;
(2)点 为线段 上方抛物线上的任意一点,过点 作 的垂线交 于点 ,点 为 轴上一点,当 的面积最大时,求 的最小值;
(3)在(2)中, 取得最小值时,将 绕点 顺时针旋转 后得到△ ,过点 作 的垂线与直线 交于点 ,点 为抛物线对称轴上的一点,在平面直角坐标系中是否存在点 ,使以点 , , , 为顶点的四边形为菱形,若存在,请直接写出点 的坐标,若不存在,请说明理由.