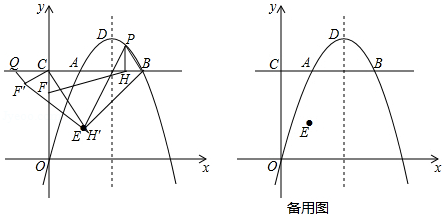
如图,在平面直角坐标系中,点在抛物线上,且横坐标为1,点与点关于抛物线的对称轴对称,直线与轴交于点,点为抛物线的顶点,点的坐标为.
(1)求线段的长;
(2)点为线段上方抛物线上的任意一点,过点作的垂线交于点,点为轴上一点,当的面积最大时,求的最小值;
(3)在(2)中,取得最小值时,将绕点顺时针旋转后得到△,过点作的垂线与直线交于点,点为抛物线对称轴上的一点,在平面直角坐标系中是否存在点,使以点,,,为顶点的四边形为菱形,若存在,请直接写出点的坐标,若不存在,请说明理由.
先化简,再求值:[(x-y)2+(x+y)(x-y)]÷2x,其中x=3,y=—1.5 .
将下列各式分解因式:(1)x3-x;(2)-x2y+2xy2-y3.
计算:5x(2x+1)—(2x+3)(5x—1)
如图,已知数轴上点A表示的数为8,B是数轴上一点,且AB=14.动点P从点A出发,以每秒5个单位长度的速度沿数轴向左匀速运动,设运动时间为t(t>0)秒.
(1)写出数轴上点B表示的数,点P表示的数(用含t的代数式表示);
(2)动点Q从点B出发,以每秒3个单位长度的速度沿数轴向左匀速运动,若点P、Q同时出发,问点P运动多少秒时追上点Q?
(3)若M为AP的中点,N为PB的中点.点P在运动的过程中,线段MN的长度是否发生变化?若变化,请说明理由;若不变,请你画出图形,并求出线段MN的长;
(4)若点D是数轴上一点,点D表示的数是x,请你探索式子 是否有最小值?如果有,直接写出最小值;如果没有,说明理由.
是否有最小值?如果有,直接写出最小值;如果没有,说明理由.
如图,O为直线AB上一点,OD平分∠AOC,∠DOE=90°.
(1)请你数一数,图中有_________个小于平角的角;
(2)若∠AOC=50°,则∠COE的度数=_________,∠BOE的度数=_________;
(3)猜想:OE是否平分∠BOC?请通过计算说明你猜想的结论.