如图,AB是⊙O的直径,BD是⊙O的弦,延长BD到点C,使DC=BD,连接AC,过点D作DE⊥AC,垂足为E.
(1)求证:AB=AC;
(2)求证:DE为⊙O的切线;
(3)若⊙O的半径为5,∠BAC=60°,求DE的长.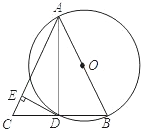
先化简,再求值: ,其中
,其中 .
.
如图1,抛物线 与
与 轴交于
轴交于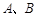 两点,与
两点,与 轴交于点
轴交于点 ,连结AC,若
,连结AC,若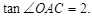

求抛物线的解析式
抛物线对称轴
 上有一动点P,当
上有一动点P,当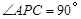 时,求出点
时,求出点 的坐标;
的坐标;如图2所示,连结
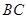 ,
,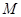 是线段
是线段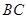 上(不与
上(不与 、
、 重合)的一个动点.过点
重合)的一个动点.过点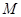 作直线
作直线 ,交抛物线于点
,交抛物线于点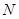 ,连结
,连结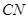 、
、 ,设点
,设点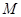 的横坐标为
的横坐标为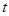 .当t为何值时,
.当t为何值时,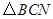 的面积最大?最大面积为多少?
的面积最大?最大面积为多少?
如图,在平面直角坐标系中,直线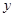 =
=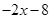 分别与
分别与 轴,
轴,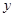 轴相交于
轴相交于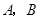 两点,点
两点,点 是
是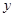 轴的负半轴上的一个动点,以
轴的负半轴上的一个动点,以 为圆心,3为半径作
为圆心,3为半径作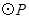 .
.连结
 ,若
,若 ,试判断
,试判断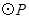 与
与 轴的位置关系,并说明理由;
轴的位置关系,并说明理由;当
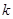 为何值时,以
为何值时,以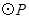 与直线
与直线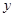 =
=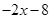 的两个交点和圆心
的两个交点和圆心 为顶点的三角形是正三角形?
为顶点的三角形是正三角形?
如图,已知正方形ABCD的边长是2,E是AB的中点,延长BC到点F使CF=AE.
求证:
 ≌
≌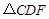 .
.把
 向左平移,使
向左平移,使 与
与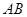 重合,得
重合,得 ,
,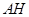 交
交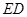 于点
于点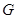 .请判断AH与ED的位置关系,并说明理由.
.请判断AH与ED的位置关系,并说明理由.求
 的长.
的长.
八年级学生到距离学校15千米的农科所参观,一部分学生骑自行车先走,过了40分钟后,其余同学乘汽车出发,结果两者同时到达.若汽车的速度是骑自行车同学速度的3倍,求骑自行车同学的速度.