某地计划用120-180天(含120与180天)的时间建设一项水利工程,工程需要运送的土石方总量为360万米3.
(1)写出运输公司完成任务所需的时间y(单位:天)与平均每天的工作量x(单位:万米3)之间的函数关系式,并给出自变量x的取值范围;
(2)由于工程进度的需要,实际平均每天运送土石比原计划多5000米3,工期比原计划减少了24天,原计划和实际平均每天运送土石方各是多少万米3?
为了解2015年祁阳县体育达标情况,县教育局从全县九年级学生中随机抽取了部分学生进行了一次体育测试(把测试结果分为四个等级:A级:优秀;B级:良好;C级:及格;D级:不及格),并将测试结果绘成了如下两幅不完整的统计图.请根据统计图中的信息解答下列问题: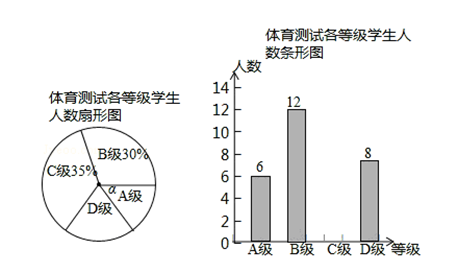
(1)本次抽样测试的学生人数是;
(2)扇形图中∠α的度数是,并把条形统计图补充完整;
(3)我县九年级有学生7200名,如果全部参加这次体育测试,请估计不及格的人数为.[来
(4)测试老师想从4位同学(分别记为E、F、G、H,其中E为小明)中随机选择两位同学了解平时训练情况,请用列表或画树状图的方法求出选中小明的概率.
已知:如图,在□ABCD中,O为对角线BD的中点,过点O的直线EF分别交AD,BC于E,F两点,连结BE,DF.
(1)求证:△DOE≌△BOF.
(2)当∠DOE等于多少度时,四边形BFED为菱形?请说明理由.
目前节能灯在城市已基本普及,今年湖南省面向县级及农村地区推广,为响应号召,某商场计划购进甲,乙两种节能灯共1200只,这两种节能灯的进价、售价如下表:
| 进价(元/只) |
售价(元/只) |
|
| 甲型 |
25 |
30 |
| 乙型 |
45 |
60 |
(1)如何进货,进货款恰好为46000元?
(2)如何进货,商场销售完节能灯时获利最多且不超过进货价的30%,此时利润为多少元
如图,我县某校新建了一座陶铸雕塑,小林站在距离雕塑2.7米的A处自B点看雕塑头顶D的仰角为45°,看雕塑底部C的仰角为30°,求塑像CD的高度.(最后结果精确到0.1米,参考数据: )
)
先化简,再求值:(a2b+ab)÷ ,其中a=
,其中a= ,b=
,b= .
.