已知函数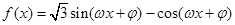
（
，
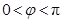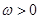）为偶函数，且函数
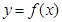图象的两相邻对称轴间的距离为
．
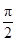(1)求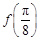
的值；
(2)将函数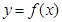的图象向右平移
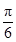个单位后，再将得到的图象上各点的横坐标伸长到原来的4倍，纵坐标不变，得到函数
的图象，求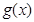
的单调递减区间．
已知函数f(x)＝alnx＋bx,且f(1)＝－1，f′(1)＝0，
⑴求f(x)；
⑵求f(x)的最大值；
⑶若x＞0,y＞0,证明：lnx＋lny≤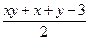
.
已知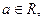
函数
．
（Ⅰ）当a＝3时，求f（x）的零点；
（Ⅱ）求函数y＝f (x)在区间 [ 1,2 ] 上的最小值．
已知函数
.
（Ⅰ）若
在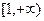
上是增函数,求实数a的取值范围.
（Ⅱ）若
是的极大值点,求在
上的最大值；
（Ⅲ）在（2）的条件下，是否存在实数b，使得函数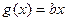
的图像与函数的图像恰有3个交点，若存在，求出b的取值范围，若不存在，说明理由.
设函数
,已知
和
为
的极值点.
(Ⅰ)求
和
的值;
(Ⅱ)讨论函数
的单调性;
(Ⅲ)设
,比较
与
的大小.
已知函数
。
（1）若
，证明：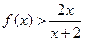
；
（2）若不等式
对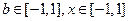
时恒成立，求实数
的取值范围。