电视传媒为了解某市100万观众对足球节目的收视情况,随机抽取了100名观众进行调查.如图是根据调查结果绘制的观众每周平均收看足球节目时间的频率分布直方图,将每周平均收看足球节目时间不低于1.5小时的观众称为“足球迷”, 并将其中每周平均收看足球节目时间不低于2.5小时的观众称为“铁杆足球迷”.
(1)试估算该市“足球迷”的人数,并指出其中“铁杆足球迷”约为多少人;
(2)该市要举办一场足球比赛,已知该市的足球场可容纳10万名观众.根据调查,如果票价定为100元/张,则非“足球迷”均不会到现场观看,而“足球迷”均愿意前往现场观看.如果票价提高 元/张
元/张 ,则“足球迷”中非“铁杆足球迷”愿意前往观看的人数会减少
,则“足球迷”中非“铁杆足球迷”愿意前往观看的人数会减少 ,“铁杆足球迷”愿意前往观看的人数会减少
,“铁杆足球迷”愿意前往观看的人数会减少 .问票价至少定为多少元/张时,才能使前往现场观看足球比赛的人数不超过10万人?
.问票价至少定为多少元/张时,才能使前往现场观看足球比赛的人数不超过10万人?
(本小题满分10分)设函数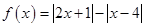 .
.
(1)解不等式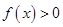 ;
;
(2)若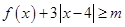 对一切实数
对一切实数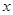 均成立,求
均成立,求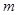 的取值范围.
的取值范围.
(本小题满分12分)已知:函数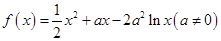
(1)求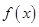 的单调区间.
的单调区间.
(2)若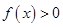 恒成立,求
恒成立,求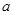 的取值范围.
的取值范围.
(本小题满分12分)已知椭圆 的左右焦点分别为
的左右焦点分别为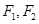 ,点
,点 在椭圆上,且
在椭圆上,且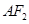 与
与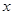 轴垂直。
轴垂直。
(1)求椭圆的方程;
(2)过 作直线与椭圆交于另外一点
作直线与椭圆交于另外一点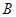 ,求
,求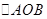 面积的最大值。
面积的最大值。
(本小题满分12分)某工厂生产 两种元件,其质量按测试指标
两种元件,其质量按测试指标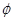 划分为:
划分为: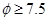 为正品,
为正品,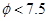 为次品.现从一批产品中随机抽取这两种元件各5件进行检测,检测结果记录如下:
为次品.现从一批产品中随机抽取这两种元件各5件进行检测,检测结果记录如下:
 |
7 |
7 |
 |
9 |
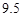 |
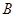 |
6 |
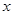 |
 |
 |
 |
由于表格被污损,数据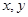 看不清,统计员只记得
看不清,统计员只记得 ,且
,且 两种元件的检测数据的平均数相等,方差也相等.
两种元件的检测数据的平均数相等,方差也相等.
(1)求表格中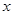 与
与 的值;
的值;
(2)若从被检测的5件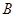 种元件中任取2件,求取出的2件都为正品的概率.
种元件中任取2件,求取出的2件都为正品的概率.
(本小题满分12分)在 中,内角
中,内角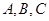 对边分别为
对边分别为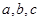 ,且
,且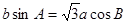
(1)求角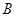 的大小;
的大小;
(2)若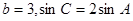 ,求
,求 的值.
的值.