如图,在四棱锥中,底面为平行四边形,,,为中点,,,为中点.

(Ⅰ)证明:;
(Ⅱ)证明:;
(Ⅲ)求直线与平面所成角的正切值.
已知函数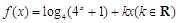 是偶函数.
是偶函数.
(1)求k的值;
(2)若方程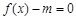 有解,求m的取值范围.
有解,求m的取值范围.
设函数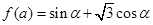 ,其中,角
,其中,角 的顶点与坐标原点重合,始边与
的顶点与坐标原点重合,始边与 轴非负半轴重合,终边经过点
轴非负半轴重合,终边经过点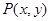 ,且
,且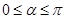 .
.
(1)若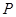 点的坐标为(-
点的坐标为(- ),求
),求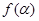 的值;
的值;
(2)若点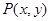 为平面区域
为平面区域 上的一个动点,试确定角
上的一个动点,试确定角 的取值范围,并求函数
的取值范围,并求函数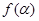 的值域.
的值域.
设命题p:函数 的定义域为R;命题q:
的定义域为R;命题q: 对一切的实数
对一切的实数 恒成立,如果命题“p且q”为假命题,求实数a的取值范围.
恒成立,如果命题“p且q”为假命题,求实数a的取值范围.
已知函数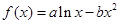 图象上一点
图象上一点 处的切线方程为
处的切线方程为 .
.
(1)求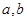 的值;
的值;
(2)若方程 在
在 内有两个不等实根,求
内有两个不等实根,求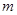 的取值范围(其中
的取值范围(其中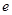 为自然对数的底数);(3)令
为自然对数的底数);(3)令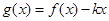 ,若
,若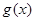 的图象与
的图象与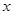 轴交于
轴交于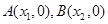 (其中
(其中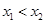 ),
),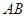 的中点为
的中点为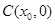 ,求证:
,求证: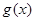 在
在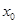 处的导数
处的导数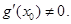
定议在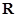 上的单调函数
上的单调函数 满足
满足 ,且对任意
,且对任意 都有
都有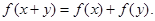
(1)求证: 为奇函数;
为奇函数;
(2)若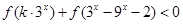 对任意
对任意 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.