如图,椭圆的中心为原点,离心率,一条准线的方程是

(Ⅰ)求椭圆的标准方程;
(Ⅱ)设动点满足:,其中、椭圆上的点,直线与的斜率之积为,
问:是否存在定点,使得与点到直线:的距离之比为定值;若存在,求的坐标,若不存在,说明理由.
设二次函数f(x)=ax2+bx+c(a,b,c∈R)满足下列条件:
①当x∈R时,f(x)的最小值为0,且f(x﹣1)=f(﹣x﹣1)恒成立;
②当x∈(0,5)时,x≤f(x)≤2|x﹣1|+1恒成立.
(1)求f(1)的值;
(2)求f(x)的解析式;
(3)求最大的实数m(m>1),使得存在实数t,只要当x∈[1,m]时,就有f(x+t)≤x成立.
已知函数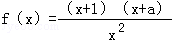 为偶函数
为偶函数
(1)求实数a的值;
(2)当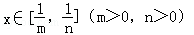 时,若函数f(x)的值域为[2﹣3m,2﹣3n],求m,n的值.
时,若函数f(x)的值域为[2﹣3m,2﹣3n],求m,n的值.
我国科研人员屠呦呦法相从青篙中提取物青篙素抗疟性超强,几乎达到100%,据监测:服药后每毫升血液中的含药量y(微克)与时间r(小时)之间近似满足如图所示的曲线
(1)写出第一服药后y与t之间的函数关系式y=f(x);
(2)据进一步测定:每毫升血液中含药量不少于 微克时,治疗有效,求服药一次后治疗有效的时间是多长?
微克时,治疗有效,求服药一次后治疗有效的时间是多长?
已知集合A={x|x2+3x﹣10≤0}
(1)若A⊆B,B={x|m﹣6≤x≤2m+1},求实数m的取值范围;
(2)若B⊆A,B={x|2m﹣1≤x≤m+1},求实数m的取值范围.
化简下列各式(写出化简过程)
(1) ;
;
(2)lg5•lg20+lg22.