甲乙两个班级均为40人,进行一门考试后,按学生考试成绩及格与不及格进行统计,甲班及格人数为36人,乙班及格人数为24人.
(1)根据以上数据建立一个 的列联表;(2)试判断成绩与班级是否有关?
的列联表;(2)试判断成绩与班级是否有关?
参考公式: ;
;
| P(K2>k) |
0.50 |
0.40 |
0.25 |
0.15 |
0.10 |
0.05 |
0.025 |
0.010 |
0.005 |
0.001 |
| k |
0.455 |
0.708 |
1.323 |
2.072 |
2.706 |
3.84 |
5.024 |
6.635 |
7.879 |
10.83 |
口袋里装有大小相同的卡片八张,其中三张标有数字1,三张标有数字2,二张标有数字3,第一次从口袋里任里任意抽取一张,放回口袋里后第二次再任意抽取一张,记第一次与第二次取到卡片上数字之和为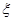 .
.
(1)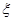 为何值时,其发生的概率最大?说明理由;
为何值时,其发生的概率最大?说明理由;
(2)求随机变量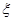 的期望
的期望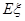 .
.
设数列 是公差大于0的等差数列,
是公差大于0的等差数列,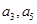 分别是方程
分别是方程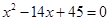 的两个实根
的两个实根
(1)求数列 的通项公式
的通项公式
(2)设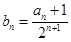 ,求数列
,求数列 的前
的前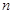 项和
项和
在 中,角
中,角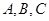 所对应的边分别为
所对应的边分别为 ,且
,且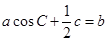
 ,
,
(1)求角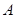 的大小
的大小
(2)若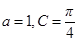 , 求
, 求 的面积
的面积
如图,圆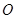 的直径
的直径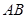 的延长线与弦
的延长线与弦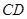 的延长线相交于点
的延长线相交于点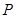 ,
,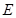 为圆
为圆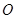 上一点,
上一点,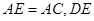 交
交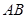 于点
于点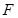 ,且
,且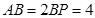
(1)求线段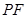 的长度
的长度
(2)若圆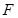 与圆
与圆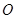 内切,直线
内切,直线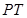 与圆
与圆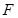 切于点
切于点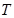 ,
,
求线段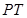 的长度
的长度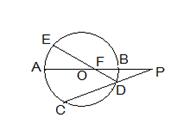
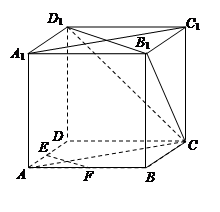
(本小题满分12分)如图,在正方体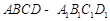 中,
中,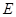 、
、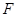 分别为棱
分别为棱 、
、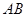 的中点.
的中点.
(1)求证:平面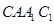 ⊥平面
⊥平面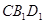 ;
;
(2)如果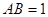 ,一个动点从点
,一个动点从点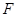 出发在正方体的表面上依次经过棱
出发在正方体的表面上依次经过棱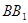 、
、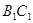 、
、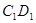 、
、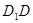 、
、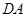 上的点,最终又回到点
上的点,最终又回到点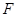 ,指出整个路线长度的最小值并说明理由.
,指出整个路线长度的最小值并说明理由.