设函数
的定义域为D，如果
，使得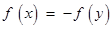
成立，则称函数为“Ω函数”. 给出下列四个函数：①
；
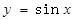②
；③
；④
, 则其中“Ω函数”共有（ ）
| A．1个 | B．2个 | C．3个 | D．4个 |
用数学归纳法证明：1+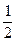
+
+
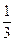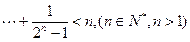时，在第二步证明从n=k到n=k+1成立时，左边增加的项数是（）
A． |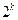
B．  |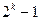
C． |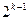
D． |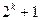
用数学归纳法证明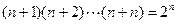
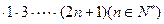，从“k到k+1”左端需乘的代数式是（）
| A．2k+1 | B． |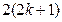
C． |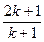
D． |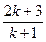
已知n是正偶数，用数学归纳法证明时，若已假设n=k（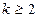
且为偶数）时命题为真，，则还需证明（）
| A．n=k+1时命题成立 | B．n=k+2时命题成立 |
| C．n=2k+2时命题成立 | D．n=2（k+2）时命题成立 |
用数学归纳法证明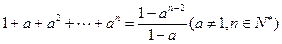
，在验证n=1时，左边计算所得的式子是（）
| A．1 | B． |
C． |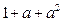
D． |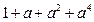
设a、b、c都是正数，则
、
、
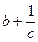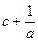三个数
| A．都大于2 | B．都小于2 | C．至少有一个大于2 | D．至少有一个不小于2 |