沿x轴正向传播的一列简谐横波在t=0时刻的波形如图所 示，M为介质中的一个质点，该波的传播速度为40 m/s，则t=
s时 （ ）(选对一个给2分，选对两个给4分，每选错一个扣2分，最低得分为0分）
| A．质点M的位移为负值 | B．质点M的速度方向与位移方向相同 . |
| C．质点M的加速度方向与速度方向相同 | D．质点M的加速度方向与位移方向相反 |
如图甲所示，光滑平行金属导轨MN、PQ所在平面与水平面成θ角，M、P两端接一阻值为R的定值电阻，阻值为r的金属棒ab垂直导轨放置，其他部分电阻不计．整个装置处在磁感应强度为B的匀强磁场中，磁场方向垂直导轨平面向上．t＝0时对金属棒施一平行于导轨的外力F，金属棒由静止开始沿导轨向上运动，通过R的感应电流随时间t变化的关系如图乙所示．下列关于穿过回路abPMa的磁通量Φ和磁通量的瞬时变化率
以及a、b两端的电势差Uab和通过金属棒的电荷量q随时间t变化的图象中，正确的是
两根相距为L的足够长的金属弯角光滑导轨如图所示放置，它们各有一边在同一水平面内，另一边与水平面的夹角为37°，质量均为m的金属细杆ab、cd与导轨垂直接触形成闭合回路，导轨的电阻不计，回路总电阻为2R，整个装置处于磁感应强度大小为B，方向竖直向上的匀强磁场中，当ab杆在平行于水平导轨的拉力F作用下以速度v沿导轨匀速运动时，cd杆恰好处于静止状态，重力加速度为g，以下说法正确的是
| A．ab杆所受拉力F的大小为mg sin37° |
B．回路中电流为 |
| C．回路中电流的总功率为mgv sin37° |
D．m与v大小的关系为m＝ |
如图所示，边长为L的正方形线圈abcd，其匝数为n，总电阻为r，外电路的电阻为R，ab的中点和cd的中点的连线OO′恰好位于匀强磁场的边界线上，磁场的磁感应强度为B.若线圈从图示位置开始，以角速度ω绕OO′轴匀速转动，则以下判断中正确的是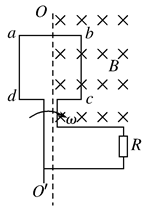
A．闭合电路中感应电动势的瞬时值表达式e＝nBL2ωsinωt
B．在t＝
时刻，磁场穿过线圈的磁通量为零，此时磁通量随时间变化最快
C．从t＝0时刻到t＝时刻，电阻R上产生的热量为Q＝n2B2L4πωR/16(R+r)2
D．从t＝0时刻到t＝时刻，通过R的电荷量q＝BL2/2R
如图，导体棒ab在宽度为d的金属导轨上运动的速度随时间变化关系
，导轨内匀强磁场的磁感强度为B，平行金属板中间固定一电子，在t=0.5s时释放电子，（电子重力不计，一切电阻均不计）则
| A．电子往复运动 （设不与板撞击） |
| B．往复运动周期为2秒（设不与板撞击） |
| C．电子作直线运动，最终到上极板 |
| D．电子作直线运动，最终到下极板 |
图甲和图乙分别表示正弦脉冲波和方波的交变电流与时间的变化关系．若使这两种电流分别通过两个完全相同的电阻，则经过1min的时间，两电阻消耗的电功之比W甲：W乙为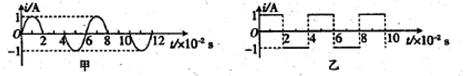 
A．1： |
B．1：2 | C．1：3 | D．1：6 |