设函数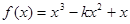
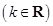 .
.
(1) 当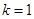 时,求函数
时,求函数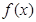 的单调区间;
的单调区间;
(2) 当 时,求函数
时,求函数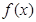 在
在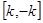 上的最小值
上的最小值 和最大值
和最大值 .
.
(满分12分)
某单位用2160万元购得一块空地,计划在该地块上建造一栋至少10层、每层2000平方米的楼房。经测算,如果将楼房建为x(x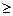 10)层,则每平方米的平均建筑费用为560+48x(单位:元)。为了使楼房每平方米的平均综合费用最少,该楼房应建为多少层?
10)层,则每平方米的平均建筑费用为560+48x(单位:元)。为了使楼房每平方米的平均综合费用最少,该楼房应建为多少层?
(注:平均综合费用=平均建筑费用+平均购地费用,平均购地费用= )
)
(满分12分) 的周长为
的周长为 ,且
,且 .
.
(1)求边 的长;
的长;
(2)若 的面积为
的面积为 ,求角
,求角 的度数.
的度数.
(满分10分)如图,A,B,C,D都在同一个与水平面垂直的平面内,B,D为两岛上的两座灯塔的塔顶。测量船于水面A处测得B点和D点的仰角分别为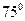 ,
,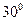 ,于水面C处测得B点和D点的仰角均为
,于水面C处测得B点和D点的仰角均为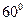 ,AC=0.1km。试探究图中B,D间距离与另外哪两点距离相等,然后求B,D的距离(计算结果保留根号).
,AC=0.1km。试探究图中B,D间距离与另外哪两点距离相等,然后求B,D的距离(计算结果保留根号).
(本小题16分)已知数列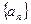 满足
满足
(1)若 ,求
,求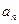 ;
;
(2)若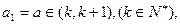 ,求
,求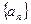 的前
的前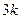 项的和
项的和 (用
(用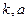 表示)
表示)
中华人民共和国《道路交通安全法》中将饮酒后违法驾驶机动车的行为分成两个档次:“酒后驾车”和“醉酒驾车”,其检测标准是驾驶人员血液中的酒精含量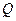 (简称血酒含量,单位是毫克/100毫升),当
(简称血酒含量,单位是毫克/100毫升),当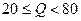 时,为酒后驾车;当
时,为酒后驾车;当 时,为醉酒驾车淮安市公安局交通管理部门于2010年6月的一天对某路段的一次拦查行动中,依法检查了200辆机动车驾驶员的血酒含量,其中查处酒后驾车的有6人,查处醉酒驾车的有4人,依据上述材料回答下列问题:
时,为醉酒驾车淮安市公安局交通管理部门于2010年6月的一天对某路段的一次拦查行动中,依法检查了200辆机动车驾驶员的血酒含量,其中查处酒后驾车的有6人,查处醉酒驾车的有4人,依据上述材料回答下列问题:
(1)分别写出违法驾车发生的频率和醉酒驾车占违法驾车总数的百分数;
(2)从违法驾车的10人中抽取4人,求抽取到醉酒驾车人数 的分布列和期望;
的分布列和期望;
(3)饮酒后违法驾驶机动车极易发生交通事故,假设酒后驾车和醉酒驾车发生交通事故的概率分别是0.2和0.5,且每位驾驶员是否发生交通事故是相互独立的,依此计算被查处的10名驾驶员中至少有一人发生交通事故的概率