如果数列
满足：
且
，则称数列为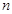
阶“归化数列”．
（1）若某4阶“归化数列”是等比数列，写出该数列的各项；
（2）若某11阶“归化数列”是等差数列，求该数列的通项公式；
（3）若为n阶“归化数列”，求证：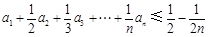
．
（本小题满分12分）
某工厂生产甲、乙两种产品，已知生产每吨甲、乙两种产品所需煤、电力、劳动力、获得利润及每天资源限额（最大供应量）如表所示：
 产品资源 |
甲产品 （每吨） |
乙产品 （每吨） |
资源限额 （每天） |
| 煤（t） |
9 |
4 |
360 |
| 电力（kw·h） |
4 |
5 |
200 |
| 劳力（个） |
3 |
10 |
300 |
| 利润（万元） |
7 |
12 |
问：每天生产甲、乙两种产品各多少吨，获得利润总额最大？
（本小题满分12分）设计一副宣传画，要求画面积为4840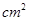
，画面的宽与高的比为
，画面的上，下各留8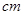
空白，左右各留5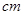空白，怎样确定画面的高于宽尺寸，能使宣传画所用纸张面积最小？
（本小题满分12分）
已知等比数列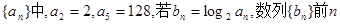
项的和为 
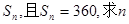的值。
（本小题满分12分）
在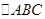
中，角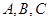
所对的边分别为
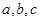且满足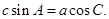
（I）求角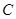
的大小；
（II）求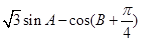
的最大值，并求取得最大值时角
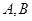的大小．
（本小题满分10分）
已知函数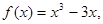
（1）求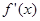
；
（2）求过点A（0，16）的曲线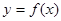
的切线方程。