已知函数 (
( R),
R), 为其导函数,且
为其导函数,且 时
时 有极小值
有极小值 .
.
(1)求 的单调递减区间;
的单调递减区间;
(2)若 ,
, ,当
,当 时,对于任意x,
时,对于任意x, 和
和 的值至少有一个是正数,求实数m的取值范围;
的值至少有一个是正数,求实数m的取值范围;
(3)若不等式 (
( 为正整数)对任意正实数
为正整数)对任意正实数 恒成立,求
恒成立,求 的最大值.
的最大值.
如图,在四棱锥 中,底面
中,底面 是菱形,
是菱形, ,
, 为
为 的中点,
的中点, 为
为 的中点.
的中点.
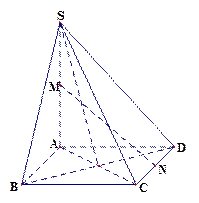
(Ⅰ)证明:平面
 平面
平面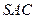 ;
;
(Ⅱ)证明:直线 .
.
已知函数f(x)=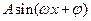 (其中A>0,
(其中A>0,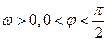 )的图象如图所示。
)的图象如图所示。
(Ⅰ)求A,w及j的值;
(Ⅱ)若tana=2,求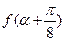 的值。
的值。
已知数列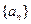 的前n项和为
的前n项和为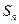 ,
, ,
,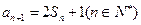 ,等差数列
,等差数列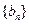 中
中
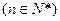 ,且
,且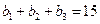 ,又
,又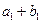 、
、 、
、 成等比数列.
成等比数列.
(Ⅰ)求数列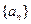 、
、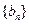 的通项公式;
的通项公式;
(Ⅱ)求数列 的前n项和
的前n项和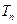 .
.
已知函数 .
.
(Ⅰ)当a=0时,求函数f(x)的图像在点A(1,f(1))处的切线方程;
(Ⅱ)若f(x)在R上单调,求a的取值范围;
(Ⅲ)当 时,求函数f(x)的极小值。
时,求函数f(x)的极小值。
在某次抽奖活动中,一个口袋里装有5个白球和5个黑球,所有球除颜色外无任何不同,每次从中摸出2个球,观察颜色后放回,若为同色,则中奖。
(Ⅰ)求仅一次摸球中奖的概率;
(Ⅱ)求连续2次摸球,恰有一次不中奖的概率;
(Ⅲ)记连续3次摸球中奖的次数为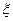 ,求
,求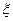 的分布列。
的分布列。